Select Goal &
City
Select Goal
Explore
Question:
A cyclist starts from the point P of a circular ground of radius 2 km and travels along its circumference to the point S. The displacement of a cyclist is :
A cyclist starts from the point P of a circular ground of radius 2 km and travels along its circumference to the point S. The displacement of a cyclist is :
Updated On: Nov 24, 2024
- 6 km
- √8 km
- 4 km
- 8 km
Hide Solution
Verified By Collegedunia
The Correct Option is B
Solution and Explanation
Since the cyclist travels along the circumference from point P to point S, which are opposite ends of the diameter of the circle, we can visualize the displacement as the straight-line distance between P and S.
1. Determine the Displacement:
- The radius R of the circular ground is given as 2 km.
- Points P and S form a diameter of the circle.
- The displacement from P to S is the length of the diagonal of the square formed by the radii OP and OS.
Using the Pythagorean theorem, we find:
\[ \text{Displacement} = R\sqrt{2} = 2\sqrt{2} = \sqrt{8} \, \text{km}. \]
Answer: \(\sqrt{8} \, \text{km}\)
Was this answer helpful?
0
0
Top Questions on Uniform Circular Motion
- A car of 800 kg is taking a turn on a banked road of radius 300 m and angle of banking 30°. If the coefficient of static friction is 0.2, then the maximum speed with which the car can negotiate the turn safely: (Given $g = 10 \, \text{m/s}^2$, $\sqrt{3} = 1.73$).
- JEE Main - 2024
- Physics
- Uniform Circular Motion
- A particle moving with uniform speed in a circular path maintains :
- NEET (UG) - 2024
- Physics
- Uniform Circular Motion
- A disc of mass \(M\) and radius \(R\) is free to rotate about its vertical axis as shown in the figure. A battery operated motor of negligible mass is fixed to this disc at a point on its circumference. Another disc of the same mass \(M\) and radius \(R/2\) is fixed to the motor’s thin shaft. Initially, both the discs are at rest. The motor is switched on so that the smaller disc rotates at a uniform angular speed \(\omega\). If the angular speed at which the large disc rotates is \(\omega/n\), then the value of \(n\) is _____
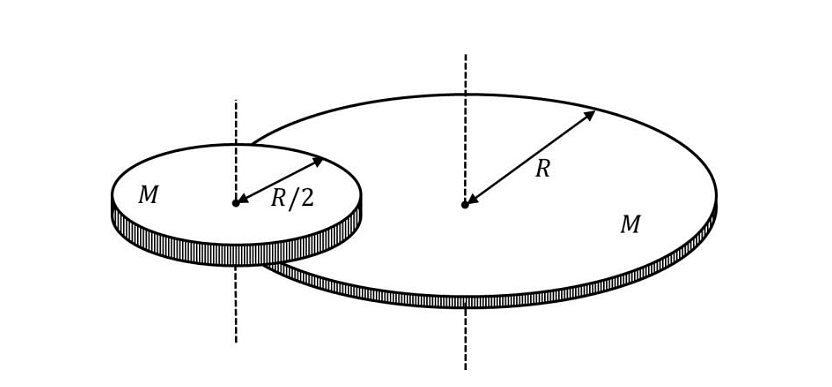
- JEE Advanced - 2024
- Physics
- Uniform Circular Motion
- A thin stiff insulated metal wire is bent into a circular loop with its two ends extending tangentially from the same point of the loop. The wire loop has mass 𝑚 and radius 𝑟 and it is in a uniform vertical magnetic field \(B_0\), as shown in the figure. Initially, it hangs vertically downwards, because of acceleration due to gravity 𝑔, on two conducting supports at P and Q. When a current 𝐼 is passed through the loop, the loop turns about the line PQ by an angle 𝜃 given by
- JEE Advanced - 2024
- Physics
- Uniform Circular Motion
- A particle connected with light thread is performing vertical circular motion. Speed at point B (Lowermost point) is sufficient, so that it is able to complete its circular motion. Ignoring air friction, find the ratio of kinetic energy at A to that at B. (A being top-most point)
- JEE Main - 2024
- Physics
- Uniform Circular Motion
View More Questions
Questions Asked in JEE Main exam
- Let \[\vec{a} = \hat{i} + \hat{j} + \hat{k}, \quad \vec{b} = -\hat{i} - 8\hat{j} + 2\hat{k}, \quad \text{and} \quad \vec{c} = 4\hat{i} + c_2\hat{j} + c_3\hat{k} \]be three vectors such that \[\vec{b} \times \vec{a} = \vec{c} \times \vec{a}.\]If the angle between the vector $\vec{c}$ and the vector $3\hat{i} + 4\hat{j} + \hat{k}$ is $\theta$, then the greatest integer less than or equal to $\tan^2 \theta$ is:
- JEE Main - 2024
- Vector Algebra
- 10 mL of gaseous hydrocarbon on combustion gives 40 mL of CO\(_2\)(g) and 50 mL of water vapour. The total number of carbon and hydrogen atoms in the hydrocarbon is ______ .
- JEE Main - 2024
- Hydrocarbons
- If each term of a geometric progression \( a_1, a_2, a_3, \dots \) with \( a_1 = \frac{1}{8} \) and \( a_2 \neq a_1 \), is the arithmetic mean of the next two terms and \( S_n = a_1 + a_2 + \dots + a_n \), then \( S_{20} - S_{18} \) is equal to
- JEE Main - 2024
- Arithmetic Mean
A body of mass 1000 kg is moving horizontally with a velocity of 6 m/s. If 200 kg extra mass is added, the final velocity (in m/s) is:
- JEE Main - 2024
- speed and velocity
- $\textbf{Choose the correct statements about the hydrides of group 15 elements.}$
A. The stability of the hydrides decreases in the order \(\text{NH}_3 > \text{PH}_3 > \text{AsH}_3 > \text{SbH}_3 > \text{BiH}_3\)
B. The reducing ability of the hydrides increases in the order \(\text{NH}_3 < \text{PH}_3 < \text{AsH}_3 < \text{SbH}_3 < \text{BiH}_3\)
C. Among the hydrides, \(\text{NH}_3\) is a strong reducing agent while \(\text{BiH}_3\) is a mild reducing agent.
D. The basicity of the hydrides increases in the order \(\text{NH}_3 < \text{PH}_3 < \text{AsH}_3 < \text{SbH}_3 < \text{BiH}_3\)
Choose the most appropriate from the option given below:- JEE Main - 2024
- p -Block Elements
View More Questions
SUBSCRIBE TO OUR NEWS LETTER
COLLEGE NOTIFICATIONSEXAM NOTIFICATIONSNEWS UPDATES
Download the Collegedunia app on 
© 2024 Collegedunia Web Pvt. Ltd. All Rights Reserved