Two capacitors $C_{1}$ and $C_{2}$ in a circuit are joined as shown in figure. The potentials of points A and B are $V_{1}$ and $V_{2}$ respectively. Then the potential of point D will be
- $\frac{\left(V_{1}+V_{2}\right)}{2}$
- $\frac{C_{2} V_{1} +C _{1}V_{2}}{C_{1}+C_{2}}$
- $\frac{C_{1}V_{1}+C_{2} V_{2}}{C_{1}+C_{2}}$
- $\frac{C_{2}V_{1}+C_{1} V_{2}}{C_{1}+C_{2}}$
The Correct Option is C
Solution and Explanation
Potential drop across $C_{1} is \, \left(V-V_{1}\right) $ and $C_{2} \, is\, \left(V_{2}-V\right)$
$\therefore\quad q_{1} =C_{1} \left(V-V_{1}\right), q_{2} =C_{2} \left(V_{2}-V\right)$
$As\, q_{1} =q_{2} \quad$ [capacitors are in series]
$\therefore\quad C_{1} \left(V-V_{1}\right)=C_{2} \left(V_{2}-V\right)$
$V=\frac{C_{1}V_{1}+C_{2} V_{2}}{C_{1}+C_{2}}$
Top Questions on Combination of capacitors

Find the equivalent capacitance across points A and B in the given electric circuit.
- JEE Main - 2023
- Physics
- Combination of capacitors
- As shown in the figure, two parallel plate capacitors having equal plate area of 200 cm2 are joined in such a way that a ≠ b. The equivalent capacitance of the combination is x ∈0 F. The value of x is_____.

- JEE Main - 2023
- Physics
- Combination of capacitors
- A parallel plate capacitor has plate area $40\, cm ^2$ and plates separation $2\, mm$ The space between the plates is filled with a dielectric medium of a thickness $1 \,mm$ and dielectric constant $5$ The capacitance of the system is :
- JEE Main - 2023
- Physics
- Combination of capacitors
- In the circuit shown in the figure, the capacitor is initially uncharged and the key K is initially open in this condition, a current of 1 A flows through the 1 Ω resistor. The key is closed at a time t=t0. Choose the correct options(given \(e^{-1}=0.36\))
- JEE Advanced - 2023
- Physics
- Combination of capacitors
- The liquid is raising at a rate of 250\(cm^3s^{-1}\) in the container. Value of the capacitance of the container after 10 sec.? (\(\varepsilon_0=9 \times10^{12}C^2N^{-1}m^{-2}\))
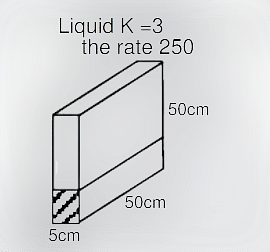
- JEE Advanced - 2023
- Physics
- Combination of capacitors
Questions Asked in VITEEE exam
- Two identical blocks A and B, each of mass 'm' resting on a smooth floor are connected by a light spring of natural length L and spring constant K, with the spring at its natural length. A third identical block 'C' (mass m) moving with a speed v along the line joining A and B collides with A. the maximum compression in the spring is
- VITEEE - 2023
- work, energy and power
- Assertion :
The binding energy of the nucleus increases with the increase in atomic number.
Reason :
Heavier elements have a greater number of non-radioactive isotopes than radioactive isotopes. - The half-life of radioactive radon is 3.8 days. The time at the end of which \(\frac{1}{20}th\) of the Radon sample will remain undecayed is (given log10e=0.4343)
- Which element has more electron gain enthalpy among chalcogen group?
- VITEEE - 2022
- sulphur
- Coin is tossed till heads is obtained what is expectation of no. of coin tosses
- VITEEE - 2022
- Random Variables
Concepts Used:
Combination of Capacitors
The total capacitance of this equivalent single capacitor depends both on the individual capacitors and how they are connected. There are two simple and common types of connections, called series and parallel, for which we can easily calculate the total capacitance.
Read Also: Combination of Capacitors
Series capacitors
When one terminal of a capacitor is connected to the terminal of another capacitors , called series combination of capacitors.
Capacitors in Parallel
Capacitors can be connected in two types which are in series and in parallel. If capacitors are connected one after the other in the form of a chain then it is in series. In series, the capacitance is less.
When the capacitors are connected between two common points they are called to be connected in parallel.
When the plates are connected in parallel the size of the plates gets doubled, because of that the capacitance is doubled. So in a parallel combination of capacitors, we get more capacitance.
Read More: Types of Capacitors



