Three blocks A, B and C are pulled on a horizontal smooth surface by a force of 80 N as shown in figure

The tensions T1 and T2 in the string are respectively:

The tensions T1 and T2 in the string are respectively:
- 40N, 64N
- 60N, 80N
- 88N, 96N
- 80N, 100N
The Correct Option is A
Solution and Explanation
Let’s analyze the forces acting on the blocks:
Calculate the Total Mass: The total mass of the system \( m \):
\[ m = m_A + m_B + m_C = 5 \, \text{kg} + 3 \, \text{kg} + 2 \, \text{kg} = 10 \, \text{kg}. \]Calculate the Acceleration of the System: Using Newton’s second law \( F = ma \):
\[ a = \frac{F}{m} = \frac{80 \, \text{N}}{10 \, \text{kg}} = 8 \, \text{m/s}^2. \]Calculate the Tension \( T_2 \) in the String Connecting B and C: For block C (mass = 2 kg), using
\[ F = ma: \] \[ T_2 = m_C \times a = 2 \, \text{kg} \times 8 \, \text{m/s}^2 = 16 \, \text{N}. \]Calculate the Tension \( T_1 \) in the String Connecting A and B: The force acting on block B (mass = 3 kg) includes both its weight and the tension \( T_2 \):
\[ T_1 = m_B \times a + T_2 = (3 \, \text{kg} \times 8 \, \text{m/s}^2) + 16 \, \text{N} = 24 \, \text{N} + 16 \, \text{N} = 40 \, \text{N}. \]Therefore, for block A (mass = 5 kg):
\[ T_1 = m_A \times a + T_1 + T_2 = (5 \, \text{kg} \times 8 \, \text{m/s}^2) = 40 \, \text{N} + T_1. \]Calculate Final Tensions: Now, substituting for \( T_2 \):
\[ T_1 = 5 \times 8 \, \text{N}, T_2 = 40 + 8 \times 3 = 64 \, \text{N}. \]Top Questions on Centre of mass
- Two solid spheres each of mass 2 kg and radius 75 cm are arranged as shown. Find MOI of the system about the given axis.
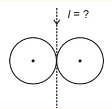
- JEE Main - 2024
- Physics
- Centre of mass
Find the value of m if \(M = 10\) \(kg\). All the surfaces are rough.
- JEE Main - 2024
- Physics
- Centre of mass
- Three identical spheres each of mass $M$ are placed at the corners of a right angled triangle with mutually perpendicular sides equal to $3 m$ each Taking point of intersection of mutually perpendicular sides as origin, the magnitude of position vector of centre of mass of the system will be $\sqrt{ x } m$ The value of $x$ is
- JEE Main - 2023
- Physics
- Centre of mass
As per the given figure, a small ball $P$ slides down the quadrant of a circle and hits the other ball $Q$ of equal mass which is initially at rest Neglecting the effect of friction and assume the collision to be elastic, the velocity of ball $Q$ after collision will be :$\left( g =10 \,m / s ^2\right)$
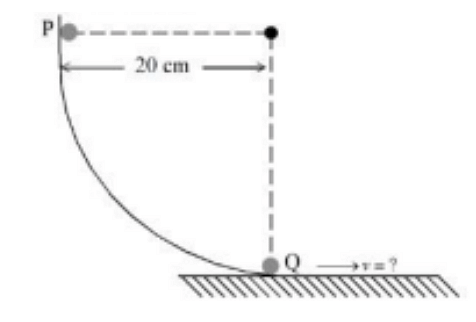
- JEE Main - 2023
- Physics
- Centre of mass
- A metal block of mass m is suspended from a rigid support through a metal wire of diameter 14 mm. The tensile stress developed in the wire under equilibrium state is 7× 105 Nm-2 . The value of mass m is ___ kg. (Take, g = 9.8 ms-2 and π =\(\frac{ 22}{7}\))
- JEE Main - 2023
- Physics
- Centre of mass
Questions Asked in JEE Main exam
- Let \[\vec{a} = \hat{i} + \hat{j} + \hat{k}, \quad \vec{b} = -\hat{i} - 8\hat{j} + 2\hat{k}, \quad \text{and} \quad \vec{c} = 4\hat{i} + c_2\hat{j} + c_3\hat{k} \]be three vectors such that \[\vec{b} \times \vec{a} = \vec{c} \times \vec{a}.\]If the angle between the vector $\vec{c}$ and the vector $3\hat{i} + 4\hat{j} + \hat{k}$ is $\theta$, then the greatest integer less than or equal to $\tan^2 \theta$ is:
- JEE Main - 2024
- Vector Algebra
- 10 mL of gaseous hydrocarbon on combustion gives 40 mL of CO\(_2\)(g) and 50 mL of water vapour. The total number of carbon and hydrogen atoms in the hydrocarbon is ______ .
- JEE Main - 2024
- Hydrocarbons
- If each term of a geometric progression \( a_1, a_2, a_3, \dots \) with \( a_1 = \frac{1}{8} \) and \( a_2 \neq a_1 \), is the arithmetic mean of the next two terms and \( S_n = a_1 + a_2 + \dots + a_n \), then \( S_{20} - S_{18} \) is equal to
- JEE Main - 2024
- Arithmetic Mean
A body of mass 1000 kg is moving horizontally with a velocity of 6 m/s. If 200 kg extra mass is added, the final velocity (in m/s) is:
- JEE Main - 2024
- speed and velocity
- $\textbf{Choose the correct statements about the hydrides of group 15 elements.}$
A. The stability of the hydrides decreases in the order \(\text{NH}_3 > \text{PH}_3 > \text{AsH}_3 > \text{SbH}_3 > \text{BiH}_3\)
B. The reducing ability of the hydrides increases in the order \(\text{NH}_3 < \text{PH}_3 < \text{AsH}_3 < \text{SbH}_3 < \text{BiH}_3\)
C. Among the hydrides, \(\text{NH}_3\) is a strong reducing agent while \(\text{BiH}_3\) is a mild reducing agent.
D. The basicity of the hydrides increases in the order \(\text{NH}_3 < \text{PH}_3 < \text{AsH}_3 < \text{SbH}_3 < \text{BiH}_3\)
Choose the most appropriate from the option given below:- JEE Main - 2024
- p -Block Elements
Concepts Used:
Center of Mass
The center of mass of a body or system of a particle is defined as a point where the whole of the mass of the body or all the masses of a set of particles appeared to be concentrated.
The formula for the Centre of Mass:

Center of Gravity
The imaginary point through which on an object or a system, the force of Gravity is acted upon is known as the Centre of Gravity of that system. Usually, it is assumed while doing mechanical problems that the gravitational field is uniform which means that the Centre of Gravity and the Centre of Mass is at the same position.



