Question:
The two curves $x^3 - 3xy^2 + 2 = 0$ and $3x^2y - y^3 = 2$
The two curves $x^3 - 3xy^2 + 2 = 0$ and $3x^2y - y^3 = 2$
Updated On: Apr 17, 2024
- Touch each other
- Cut each other at right angle
- Cut at an angle $\pi / 3$
- Cut at an angle $\pi / 4$
Hide Solution
Verified By Collegedunia
The Correct Option is B
Solution and Explanation
We have, $x^{3}-3 x y^{2}+2=0$
$\Rightarrow 3 x^{2}-6 x y \frac{d y}{d x}-3 y^{2}=0$
$\Rightarrow \frac{d y}{d x}=\frac{3\left(x^{2}-y^{2}\right)}{6 x y}$
Now, $\left(\frac{d y}{d x}\right)_{(h, k)}=\frac{3\left(h^{2}-k^{2}\right)}{6 h k}=m_{1}$[say]
and $3 x^{2} y-y^{8}=2$
$\Rightarrow 3 x^{2} \frac{d y}{d x}+6 x y-3 y^{2} \frac{d y}{d x}=0$
$\Rightarrow \frac{d y}{d x}=\frac{-6 x y}{3\left(x^{2}-y^{2}\right)}$
Now, $\left(\frac{d y}{d x}\right)_{(h, h)}=\frac{-6 h k}{3\left(h^{2}-k^{2}\right)}=m_{2}$[say]
$\therefore m_{1} \cdot m_{2}=\frac{3\left(h^{2}-k^{2}\right)}{6 h k} \times \frac{-6 h k}{3\left(h^{2}-k^{2}\right)}=-1$
Hence, both the curves cut each other at right angle.
$\Rightarrow 3 x^{2}-6 x y \frac{d y}{d x}-3 y^{2}=0$
$\Rightarrow \frac{d y}{d x}=\frac{3\left(x^{2}-y^{2}\right)}{6 x y}$
Now, $\left(\frac{d y}{d x}\right)_{(h, k)}=\frac{3\left(h^{2}-k^{2}\right)}{6 h k}=m_{1}$[say]
and $3 x^{2} y-y^{8}=2$
$\Rightarrow 3 x^{2} \frac{d y}{d x}+6 x y-3 y^{2} \frac{d y}{d x}=0$
$\Rightarrow \frac{d y}{d x}=\frac{-6 x y}{3\left(x^{2}-y^{2}\right)}$
Now, $\left(\frac{d y}{d x}\right)_{(h, h)}=\frac{-6 h k}{3\left(h^{2}-k^{2}\right)}=m_{2}$[say]
$\therefore m_{1} \cdot m_{2}=\frac{3\left(h^{2}-k^{2}\right)}{6 h k} \times \frac{-6 h k}{3\left(h^{2}-k^{2}\right)}=-1$
Hence, both the curves cut each other at right angle.
Was this answer helpful?
0
0
Top Questions on Application of derivatives
- \(y=f(x)\) is a quadratic function passing through (–1, 0) and tangent to it at (1, 1) is \(y=x\). Find x intercept by normal at point (𝛂, 𝛂 + 1), (𝛂 > 0)
- JEE Main - 2023
- Mathematics
- Application of derivatives
Area of region enclosed by curve y=x3 and its tangent at (–1,–1)
- JEE Main - 2023
- Mathematics
- Application of derivatives
- Let $y=f(x)=\sin ^3\left(\frac{\pi}{3}\left(\cos \left(\frac{\pi}{3 \sqrt{2}}\left(-4 x^3+5 x^2+1\right)^{\frac{3}{2}}\right)\right)\right)$ Then, at $x=1$
- JEE Main - 2023
- Mathematics
- Application of derivatives
- Let $x=2$ be a local minima of the function $f(x)=2 x^4-18 x^2+8 x+12$, $x \in(-4,4)$ If $M$ is local maximum value of the function $f$ in $(-4,4)$, then $M =$
- JEE Main - 2023
- Mathematics
- Application of derivatives
- Let $x=2$ be a local minima of the function $f(x)=2 x^4-18 x^2+8 x+12$, $x \in(-4,4)$ If $M$ is local maximum value of the function $f$ in $(-4,4)$, then $M =$
- JEE Main - 2023
- Mathematics
- Application of derivatives
View More Questions
Questions Asked in KCET exam
- The current in a coil changes from 2A to 5A in 0.3s. The magnitude of emf induced in the coil is 1.0V. The value of self-inductance of the coil is
- KCET - 2023
- Electromagnetic induction
- A stretched wire of a material whose Young's modulus Y = 2 × 1011 Nm-2 has Poisson's ratio of 0.25. Its lateral strain εl = 10-3. The elastic energy density of the wire is
- KCET - 2023
- mechanical properties of solids
- A particle moves along the curve \(\frac{x^2}{16}+\frac{y^2}{4}=1\). When the rate of change of abscissa is 4 times that of its ordinate, then the quadrant in which the particle lies is
- KCET - 2023
- Conic sections
- A point object is moving at a constant speed of 1 ms-1 along the principal axis of a convex lens of focal length 10cm. The speed of the image is also 1 ms-1 , when the object is at _______ cm from the optic centre of the lens.
- KCET - 2023
- spherical lenses
- A cubical Gaussian surface has side of length a = 10 cm. Electric field lines are parallel to x-axis as shown. The magnitudes of electric fields through surfaces ABCD and EFGH are 6kNC-1 and 9kNC-1 respectively. Then the total charge enclosed by the cube is
[Take ε0 = 9 × 10-12 Fm-1]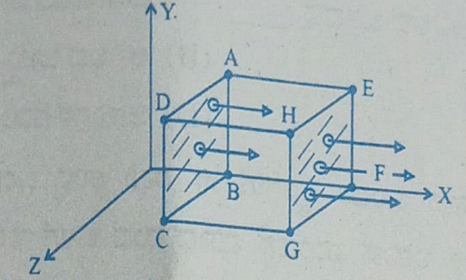
- KCET - 2023
- Gauss Law
View More Questions
Concepts Used:
Application of Derivatives
Various Applications of Derivatives-
Rate of Change of Quantities:
If some other quantity ‘y’ causes some change in a quantity of surely ‘x’, in view of the fact that an equation of the form y = f(x) gets consistently pleased, i.e, ‘y’ is a function of ‘x’ then the rate of change of ‘y’ related to ‘x’ is to be given by
\(\frac{\triangle y}{\triangle x}=\frac{y_2-y_1}{x_2-x_1}\)
This is also known to be as the Average Rate of Change.
Increasing and Decreasing Function:
Consider y = f(x) be a differentiable function (whose derivative exists at all points in the domain) in an interval x = (a,b).
- If for any two points x1 and x2 in the interval x such a manner that x1 < x2, there holds an inequality f(x1) ≤ f(x2); then the function f(x) is known as increasing in this interval.
- Likewise, if for any two points x1 and x2 in the interval x such a manner that x1 < x2, there holds an inequality f(x1) ≥ f(x2); then the function f(x) is known as decreasing in this interval.
- The functions are commonly known as strictly increasing or decreasing functions, given the inequalities are strict: f(x1) < f(x2) for strictly increasing and f(x1) > f(x2) for strictly decreasing.
Read More: Application of Derivatives



