The schematic diagram below shows 12 rectangular houses in a housing complex. House numbers are mentioned in the rectangles representing the houses. The houses are located in six columns - Column-A through Column-F, and two rows - Row-1 and Row- 2 . The houses are divided into two blocks - Block XX and Block YY. The diagram also shows two roads, one passing in front of the houses in Row-2 and another between the two blocks.

Some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The road adjacency value of a house is the number of its sides adjacent to a road. For example, the road adjacency values of C2, F2, and B1 are 2, 1, and 0, respectively. The neighbour count of a house is the number of sides of that house adjacent to occupied houses in the same block. For example, E1 and C1 can have the maximum possible neighbour counts of 3 and 2, respectively.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbour count).
The following information is also known.
1. The maximum quoted price of a house in Block XX is Rs. 24 lakhs. The minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column-E.
2. Row-1 has two occupied houses, one in each block.
3. Both houses in Column-E are vacant. Each of Column-D and Column-F has at least one occupied house.
4. There is only one house with parking space in Block YY.
What is the maximum possible quoted price (in lakhs of Rs.) for a vacant house in Column-E? [This question was asked as TITA]

Some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The road adjacency value of a house is the number of its sides adjacent to a road. For example, the road adjacency values of C2, F2, and B1 are 2, 1, and 0, respectively. The neighbour count of a house is the number of sides of that house adjacent to occupied houses in the same block. For example, E1 and C1 can have the maximum possible neighbour counts of 3 and 2, respectively.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbour count).
The following information is also known.
1. The maximum quoted price of a house in Block XX is Rs. 24 lakhs. The minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column-E.
2. Row-1 has two occupied houses, one in each block.
3. Both houses in Column-E are vacant. Each of Column-D and Column-F has at least one occupied house.
4. There is only one house with parking space in Block YY.
What is the maximum possible quoted price (in lakhs of Rs.) for a vacant house in Column-E? [This question was asked as TITA]
- 20 lakhs
- 22 lakhs
- 23 lakhs
- 21 lakhs
The Correct Option is D
Approach Solution - 1
The correct answer is 21.
Approach Solution -2
Given: The price for an empty house is either Rs. 10 lakhs if it doesn't have a parking spot or Rs. 12 lakhs if it does.
In Block YY, both E1 and E2 are vacant, and one of them costs 15 lakhs. Let's focus on E1.
For E1:
Neighbor count = 1 (exactly one of D1 or F1 is occupied)
Road adjacency = 0
So, the cost of E1 would be: \((10 \text{ or } 12) + 5 \times 0 + 3 \times 1 = 13 \text{ or } 15\) lakhs.
Since 15 lakhs is the lowest cost for a house in Block YY, E1 must cost 15 lakhs. This implies E1 is the only house in YY with a parking space.
let's calculate the maximum possible price of E2.
E2's base price is 10 lakhs since it cannot have a parking space (only one house in YY, E1, has a parking space). The road adjacency for E2 is 1, and the maximum neighbor count of E2 will be 2 (both D2 and F2 are occupied, and E1 is vacant).
So, E2's price would be: \(10 + 5 \times 1 + 3 \times 2 = 21\) lakhs.
Hence, the maximum possible price for E2 is 21 lakhs.
So, the correct option is (D): 21 lakhs.
Top Questions on Data Analysis
- How many boxes have at least one sack containing 9 coins?
- _____ the shape of the data set to make it suitable for analysis.
- CUET (UG) - 2023
- Computer Science
- Data Analysis
- The schematic diagram below shows 12 rectangular houses in a housing complex. House numbers are mentioned in the rectangles representing the houses. The houses are located in six columns - Column-A through Column-F, and two rows - Row-1 and Row- 2 . The houses are divided into two blocks - Block XX and Block YY. The diagram also shows two roads, one passing in front of the houses in Row-2 and another between the two blocks.

Some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The road adjacency value of a house is the number of its sides adjacent to a road. For example, the road adjacency values of C2, F2, and B1 are 2, 1, and 0, respectively. The neighbour count of a house is the number of sides of that house adjacent to occupied houses in the same block. For example, E1 and C1 can have the maximum possible neighbour counts of 3 and 2, respectively.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbour count).
The following information is also known.
1. The maximum quoted price of a house in Block XX is Rs. 24 lakhs. The minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column-E.
2. Row-1 has two occupied houses, one in each block.
3. Both houses in Column-E are vacant. Each of Column-D and Column-F has at least one occupied house.
4. There is only one house with parking space in Block YY.
How many houses are vacant in Block XX? [This question was asked as TITA] - There are only three female students - Amala, Koli and Rini - and only three male students - Biman, Mathew and Shyamal - in a course. The course has two evaluation components, a project and a test. The aggregate score in the course is a weighted average of the two components, with the weights being positive and adding to 1 .
The projects are done in groups of two, with each group consisting of a female and a male student. Both the group members obtain the same score in the project.
The following additional facts are known about the scores in the project and the test.
1. The minimum, maximum and the average of both project and test scores were identical – 40, 80 and 60 , respectively.
2. The test scores of the students were all multiples of 10 ; four of them were distinct and the remaining two were equal to the average test scores.
3. Amala's score in the project was double that of Koli in the same, but Koli scored 20 more than Amala in the test. Yet Amala had the highest aggregate score.
4. Shyamal scored the second highest in the test. He scored two more than Koli, but two less than Amala in the aggregate.
5. Biman scored the second lowest in the test and the lowest in the aggregate.
6. Mathew scored more than Rini in the project, but less than her in the test.
What was Rini's score in the project?(This Question was asked as TITA) - There are nine boxes arranged in a 3×3 array as shown in Tables 1 and 2. Each box contains three sacks. Each sack has a certain number of coins, between 1 and 9, both inclusive.
The average number of coins per sack in the boxes are all distinct integers. The total number of coins in each row is the same. The total number of
coins in each column is also the same.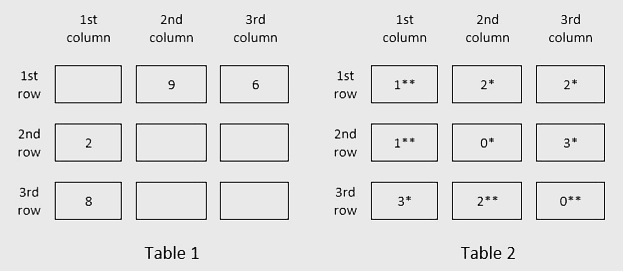
Table 1 gives information regarding the median of the numbers of coins in the three sacks in a box for some of the boxes. In Table 2 each box has a number which represents the number of sacks in that box having more than 5 coins. That number is followed by a * if the sacks in that box satisfy exactly one among the following three conditions, and it is followed by ** if two or more of these conditions are satisfied.
i) The minimum among the numbers of coins in the three sacks in the box is 1.
ii) The median of the numbers of coins in the three sacks is 1.
iii) The maximum among the numbers of coins in the three sacks in the box is 9.
In how many boxes do all three sacks contain different numbers of coins? [This Question was asked as TITA]
Questions Asked in CAT exam
- If Rajesh’s age were to be the present age of Shivani, their age ratio would be \(3:2\). Then what would be their present age ratio?
- CAT - 2024
- Ratio and Proportion
- A shopkeeper sells half of the grains plus \(3 \, \text{kg}\) of grains to Customer 1, and then sells another half of the remaining grains plus \(3 \, \text{kg}\) to Customer 2. When the 3rd customer arrives, there are no grains left. Find the total grains that were initially present.
- CAT - 2024
- Sequence and Series
- Read the Passage carefully and answer the following questions.
An air conditioner (AC) unit has three operating modes: Eco, Normal, and Turbo. The power consumption in each mode is as follows: Eco mode consumes 1000 watts, Normal mode consumes 1200 watts, and Turbo mode consumes 1500 watts. Yesterday, the AC was in operation from 2 PM to 10 PM. From 2 PM to 6 PM it ran in Eco mode. From 6 PM to 8 PM, it ran in Normal mode. From 8 PM to 10 PM it ran in Turbo mode.- CAT - 2024
- Data Interpretation
- Read the Passage carefully and answer the following questions
A health food store specializing in dietary supplements and whole grains recorded the following sales figures (in kilograms) for various food categories last month: Millets (M) = 500 kg at a cost price of 40/kg and selling price of 50/kg; Protein supplements (P) = 300 kg at a cost price of 80/kg and selling price of 100/kg; Vitamin supplements (V) = 200 kg at a cost price of 60/kg and selling price of 80/kg; Carbohydrates (C) = 600 kg at a cost price of 80/kg and selling price of 100/kg; Fats (F) = 100 kg at a cost price of 120/kg and selling price of 150/kg. Additionally, they sold 50 kg of mixed nuts (N) at a cost price of 100/kg and a selling price of 130/kg- CAT - 2024
- Data Interpretation
- Analyse the bar graph carefully and answer the following questions.

- CAT - 2024
- Bar Graph



