Question:
The general solution of the differential equation is
The general solution of the differential equation is
Updated On: Apr 20, 2024
- (A) (a + bx)e5x
- (B) (ax + b)e–4x
- (C) (a + bx2)e4x
- (D) (a + bx4)e4x
Hide Solution
Verified By Collegedunia
The Correct Option is B
Solution and Explanation
Explanation:
Was this answer helpful?
0
0
Top Questions on Vectors
- The least positive integral value of \( \alpha \), for which the angle between the vectors \( \alpha \hat{i} - 2\hat{j} + 2\hat{k} \) and \( \alpha \hat{i} + 2\alpha \hat{j} - 2\hat{k} \) is acute, is ______.
- Let \(\vec{a} = \hat{i} + 2\hat{j} + \hat{k}\), \(\vec{b} = 3(\hat{i} - \hat{j} + \hat{k})\). Let \(\vec{c}\) be the vector such that \(\vec{a} \times \vec{c} = \vec{b}\) and \(\vec{a} \cdot \vec{c} = 3\). Then \(\vec{a} \cdot ((\vec{c} \times \vec{b}) - \vec{b} \cdot \vec{c})\) is equal to:
- Let \( A (2, 3, 5) \) and \( C(-3, 4, -2) \) be opposite vertices of a parallelogram \( ABCD \). If the diagonal \( \overrightarrow{BD} = \hat{i} + 2 \hat{j} + 3 \hat{k} \), then the area of the parallelogram is equal to
- Let \( \vec{a} = a_1 \hat{i} + a_2 \hat{j} + a_3 \hat{k} \) and \( \vec{b} = b_1 \hat{i} + b_2 \hat{j} + b_3 \hat{k} \) be two vectors such that \( |\vec{a}| = 1 \), \( \vec{a} \times \vec{b} = 2 \), and \( |\vec{b}| = 4 \). If \( \vec{c} = 2(\vec{a} \times \vec{b}) - 3\vec{b} \), then the angle between \( \vec{b} \) and \( \vec{c} \) is equal to:
- Consider a vector field \( \vec{F} = (2xz + 3y^2)\hat{y} + 4yz^2\hat{z} \). The closed path (\( \Gamma \): \( A \rightarrow B \rightarrow C \rightarrow D \rightarrow A \)) in the \( z = 0 \) plane is shown in the figure.
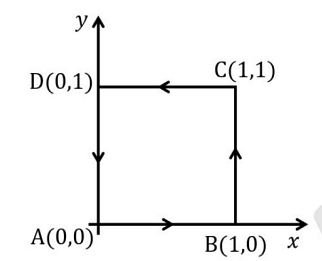
\( \oint_\Gamma \vec{F} \cdot d\vec{l} \) denotes the line integral of \( \vec{F} \) along the closed path \( \Gamma \). Which of the following options is/are true?
View More Questions
Questions Asked in WBJEE exam
- Three identical convex lenses each of focal length f are placed in a straight line separated by a distance f from each other. An object is located in \(\frac{f}{2}\) in front of the leftmost lens. Then,

- WBJEE - 2023
- Ray optics and optical instruments
- \(\lim_{x\rightarrow \infty}\){\(x-\sqrt[n]{(x-a_1)(x-a_2)......(x-a_n)}\)} where a1,a2,.....an are positive rational numbers.The limit
- A particle of mass m is projected at velocity at a velocity u, making an angle θ with the horizontal(x-axis). If the angle of projection θ is varied keeping all other parameters same, then magnitude of angular momentum(L) at its maximum height about the point of projection varies with θ as,
- WBJEE - 2023
- System of Particles & Rotational Motion
- If \(\int \frac{dx}{(x+1)(x-2)(x-3)}=\frac{1}{k}log_e\left \{ \frac{|x-3|^3|x+1|}{(x-2)^4}\right \}+c\), then the value of k is
- WBJEE - 2023
- Integrals of Some Particular Functions
- A rectangle ABCD has its side parallel to the line y=2x and vertices A,B,D are on y=1,x=1 and x=-1 respectively. The coordinate of C can be
- WBJEE - 2023
- Straight lines
View More Questions



