The elastic behavior of material for linear stress and linear strain, is shown in the figure. The energy density for a linear strain of 5×10–4 is ____ kJ/m3. Assume that material is elastic up to the linear strain of 5×10–4
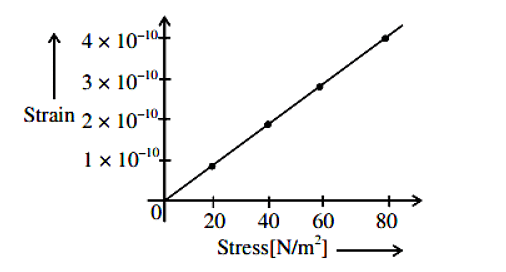
The elastic behavior of material for linear stress and linear strain, is shown in the figure. The energy density for a linear strain of 5×10–4 is ____ kJ/m3. Assume that material is elastic up to the linear strain of 5×10–4
Correct Answer: 25
Solution and Explanation
\(\mu_d = \frac{1}{2} \times \Upsilon \times (\text{strain})^2\)
\(\frac{1}{2} \times \left( \frac{20}{10^{ - 10} }\right) \times \left(5 \times 10^{-4}\right)^2 \)
= \(10^{11} × 25 × 10^{–8} \)
\(= 25 × 10^3 J/m^3\)
\(= 25\ kJ/m^3\)
Top Questions on elastic moduli
- If the length of a wire is made double and radius is halved of its respective values. Then, the Young’s modulus of the material of the wire will :
- JEE Main - 2022
- Physics
- elastic moduli
- A wire of length L and radius r is clamped rigidly at one end. When the other end of the wire is pulled by a force F, its length increases by 5 cm. Another wire of the same material of length 4L and radius 4r is pulled by a force 4F under same conditions. The increase in length of this wire is ___ cm.
- JEE Main - 2022
- Physics
- elastic moduli
- A screw gauge gives the following readings when used to measure the diameter of a wire Main scale reading : $0\, mm$ Circular scale reading : $52$ divisions Given that $1\, mm$ on main scale corresponds to $100$ divisions on the circular scale. The diameter of the wire from the above data is :
- NEET (UG) - 2021
- Physics
- elastic moduli
- When a body is strained, energy stored per unit volume is (Y-Young's modulus)
- KEAM - 2021
- Physics
- elastic moduli
- The TRUE statement is
- KEAM - 2021
- Physics
- elastic moduli
Questions Asked in JEE Main exam
- An artificial cell is made by encapsulating \(0.2 \, \text{M}\) glucose solution within a semipermeable membrane. The osmotic pressure developed when the artificial cell is placed within a \(0.05 \, \text{M}\) solution of NaCl at 300 K is ______ \( \times 10^{-1} \, \text{bar} \). (Nearest Integer)
Given: \(R = 0.083 \, \text{L bar mol}^{-1} \text{K}^{-1}\)
Assume complete dissociation of NaCl.- JEE Main - 2024
- Colligative Properties
- Let \[\vec{a} = \hat{i} + \hat{j} + \hat{k}, \quad \vec{b} = -\hat{i} - 8\hat{j} + 2\hat{k}, \quad \text{and} \quad \vec{c} = 4\hat{i} + c_2\hat{j} + c_3\hat{k} \]be three vectors such that \[\vec{b} \times \vec{a} = \vec{c} \times \vec{a}.\]If the angle between the vector $\vec{c}$ and the vector $3\hat{i} + 4\hat{j} + \hat{k}$ is $\theta$, then the greatest integer less than or equal to $\tan^2 \theta$ is:
- JEE Main - 2024
- Vector Algebra
- 10 mL of gaseous hydrocarbon on combustion gives 40 mL of CO\(_2\)(g) and 50 mL of water vapour. The total number of carbon and hydrogen atoms in the hydrocarbon is ______ .
- JEE Main - 2024
- Hydrocarbons
- If each term of a geometric progression \( a_1, a_2, a_3, \dots \) with \( a_1 = \frac{1}{8} \) and \( a_2 \neq a_1 \), is the arithmetic mean of the next two terms and \( S_n = a_1 + a_2 + \dots + a_n \), then \( S_{20} - S_{18} \) is equal to
- JEE Main - 2024
- Arithmetic Mean
A body of mass 1000 kg is moving horizontally with a velocity of 6 m/s. If 200 kg extra mass is added, the final velocity (in m/s) is:
- JEE Main - 2024
- speed and velocity
Concepts Used:
Elastic Moduli
Elastic moduli, also known as modulus of elasticity, are mechanical properties of materials that describe their ability to resist deformation under an applied load. They are used to quantify the stress-strain relationship of a material.
There are three main types of elastic moduli: Young's modulus (E), shear modulus (G), and bulk modulus (K). Young's modulus is a measure of a material's stiffness in tension or compression, while shear modulus is a measure of its resistance to shear deformation. Bulk modulus is a measure of its resistance to compression.
These moduli are important in many areas of engineering and physics, as they govern the behavior of materials under different types of loading conditions. For example, Young's modulus is used to design and analyze structures such as bridges and buildings, while shear modulus is important in the study of earthquakes and the behavior of soils.
The elastic moduli of a material are dependent on its microstructure, such as its crystal structure, grain size, and defects. They are also influenced by temperature, pressure, and other environmental factors.
The study and measurement of elastic moduli are essential for understanding the mechanical properties of materials, as well as for the design and analysis of structures and devices in engineering and physics.



