Question:
Let $S=\frac{2}{1} ^{n}C_{0}+\frac{2^{2}}{2} ^{n}C_{1}+\frac{2^{3}}{3} ^{n}C_{2}+ ...... +\frac{2^{n+1}}{n+1} ^{n}C_{n}$. Then $S$ equals
Let $S=\frac{2}{1} ^{n}C_{0}+\frac{2^{2}}{2} ^{n}C_{1}+\frac{2^{3}}{3} ^{n}C_{2}+ ...... +\frac{2^{n+1}}{n+1} ^{n}C_{n}$. Then $S$ equals
Updated On: Jun 18, 2022
- $\frac{2^{n+1}-1}{n+1}$
- $\frac{3^{n+1}-1}{n+1}$
- $\frac{3^n-1}{n}$
- $\frac{2^{n}-1}{n}$
Hide Solution
Verified By Collegedunia
The Correct Option is B
Solution and Explanation
We know that
$(1+x)^{n}={ }^{n} C_{0}+x{ }^{n} C_{1}+x^{2}{ }^{n} C_{2}+\ldots+x^{n}{ }^{n} C_{n}$
On integrating both sides from 0 to 2 , we get
$\left[\frac{(1+x)^{n+1}}{n+1}\right]_{0}^{2}$
$=\left[x^{n} C_{0}+\frac{x^{2}}{2}{ }^{n} C_{1}+\frac{x^{3}}{3}{ }^{n} C_{2}+\ldots+\frac{x^{n+1}}{n+1}{ }^{n} C_{n}\right]_{0}^{2}$
$\Rightarrow \frac{(3)^{n+1}}{n+1}-\frac{1}{n+1}=2{ }^{n} C_{0}+\frac{2^{2}}{2}{ }^{n} C_{1}+\frac{2^{3}}{3}{ }^{n} C_{2}+\ldots+\frac{2^{n+1}}{n+1}{ }^{n} C_{n}-0$
$\Rightarrow \frac{2}{1}{ }^{n} C_{0}+\frac{2^{2}}{2}{ }^{n} C_{1}+\frac{2^{3}}{3}{ }^{n} C_{2}+\ldots+\frac{2^{n+1}}{n+1}{ }^{n} C_{n}$
$=\frac{3^{n+1}-1}{n+1}$
$(1+x)^{n}={ }^{n} C_{0}+x{ }^{n} C_{1}+x^{2}{ }^{n} C_{2}+\ldots+x^{n}{ }^{n} C_{n}$
On integrating both sides from 0 to 2 , we get
$\left[\frac{(1+x)^{n+1}}{n+1}\right]_{0}^{2}$
$=\left[x^{n} C_{0}+\frac{x^{2}}{2}{ }^{n} C_{1}+\frac{x^{3}}{3}{ }^{n} C_{2}+\ldots+\frac{x^{n+1}}{n+1}{ }^{n} C_{n}\right]_{0}^{2}$
$\Rightarrow \frac{(3)^{n+1}}{n+1}-\frac{1}{n+1}=2{ }^{n} C_{0}+\frac{2^{2}}{2}{ }^{n} C_{1}+\frac{2^{3}}{3}{ }^{n} C_{2}+\ldots+\frac{2^{n+1}}{n+1}{ }^{n} C_{n}-0$
$\Rightarrow \frac{2}{1}{ }^{n} C_{0}+\frac{2^{2}}{2}{ }^{n} C_{1}+\frac{2^{3}}{3}{ }^{n} C_{2}+\ldots+\frac{2^{n+1}}{n+1}{ }^{n} C_{n}$
$=\frac{3^{n+1}-1}{n+1}$
Was this answer helpful?
0
0
Top Questions on Integrals of Some Particular Functions
- If \(\int \frac{dx}{(x+1)(x-2)(x-3)}=\frac{1}{k}log_e\left \{ \frac{|x-3|^3|x+1|}{(x-2)^4}\right \}+c\), then the value of k is
- WBJEE - 2023
- Mathematics
- Integrals of Some Particular Functions
- Let $f(x)=\int \frac{2 x}{\left(x^2+1\right)\left(x^2+3\right)} d x$ If $f(3)=\frac{1}{2}\left(\log _e 5-\log _e 6\right)$, then $f(4)$ is equal to
- JEE Main - 2023
- Mathematics
- Integrals of Some Particular Functions
- If $\int \sqrt{\sec 2 x-1} d x=\alpha \log _e\left|\cos 2 x+\beta+\sqrt{\cos 2 x\left(1+\cos \frac{1}{\beta} x\right)}\right|+$ constant, then $\beta-\alpha$ is equal to_______
- JEE Main - 2023
- Mathematics
- Integrals of Some Particular Functions
- If $\int \limits_0^\pi \frac{5^{\cos x}\left(1+\cos x \cos 3 x+\cos ^2 x+\cos ^3 x \cos 3 x\right) d x}{1+5^{\cos x}}=\frac{ k \pi}{16}$, then $k$ is equal to
- JEE Main - 2023
- Mathematics
- Integrals of Some Particular Functions
- The integral $16 \int\limits_1^2 \frac{d x}{x^3\left(x^2+2\right)^2}$ is equal to
- JEE Main - 2023
- Mathematics
- Integrals of Some Particular Functions
View More Questions
Questions Asked in WBJEE exam
- Three identical convex lenses each of focal length f are placed in a straight line separated by a distance f from each other. An object is located in \(\frac{f}{2}\) in front of the leftmost lens. Then,

- WBJEE - 2023
- Ray optics and optical instruments
- \(\lim_{x\rightarrow \infty}\){\(x-\sqrt[n]{(x-a_1)(x-a_2)......(x-a_n)}\)} where a1,a2,.....an are positive rational numbers.The limit
- A particle of mass m is projected at velocity at a velocity u, making an angle θ with the horizontal(x-axis). If the angle of projection θ is varied keeping all other parameters same, then magnitude of angular momentum(L) at its maximum height about the point of projection varies with θ as,
- WBJEE - 2023
- System of Particles & Rotational Motion
- A rectangle ABCD has its side parallel to the line y=2x and vertices A,B,D are on y=1,x=1 and x=-1 respectively. The coordinate of C can be
- WBJEE - 2023
- Straight lines
- In an experiment on a circuit, as shown in the figure, the voltmeter shows 8V reading. The resistance of the voltmeter is
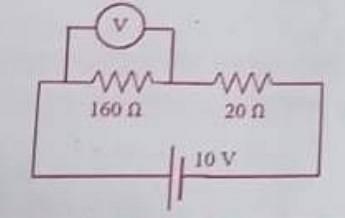
- WBJEE - 2023
- Resistance
View More Questions
Concepts Used:
Integrals of Some Particular Functions
There are many important integration formulas which are applied to integrate many other standard integrals. In this article, we will take a look at the integrals of these particular functions and see how they are used in several other standard integrals.
Integrals of Some Particular Functions:
- ∫1/(x2 – a2) dx = (1/2a) log|(x – a)/(x + a)| + C
- ∫1/(a2 – x2) dx = (1/2a) log|(a + x)/(a – x)| + C
- ∫1/(x2 + a2) dx = (1/a) tan-1(x/a) + C
- ∫1/√(x2 – a2) dx = log|x + √(x2 – a2)| + C
- ∫1/√(a2 – x2) dx = sin-1(x/a) + C
- ∫1/√(x2 + a2) dx = log|x + √(x2 + a2)| + C
These are tabulated below along with the meaning of each part.




