Let P be a point on the parabola y2 = 4ax, where a > 0. The normal to the parabola at P meets the x -axis at a point Q. The area of the triangle PFQ where F is the focus of the parabola, is 120. If the slope m of the normal and a are both positive integers, then the pair (a, m) is
Let P be a point on the parabola y2 = 4ax, where a > 0. The normal to the parabola at P meets the x -axis at a point Q. The area of the triangle PFQ where F is the focus of the parabola, is 120. If the slope m of the normal and a are both positive integers, then the pair (a, m) is
(2,3)
(1,3)
(2,4)
(3,4)
The Correct Option is A
Approach Solution - 1

Equation of normal at P(am2, –2am) is y = mx – 2am – am3
⇒ Area of ∆PFQ = 1/2(a + am2) x 2am = 120
a2m(1 + m2) = 120 Pair (a, m) ≡ (2, 3) satisfies above equation.
Approach Solution -2

Given :
y2 = 4ax
Now, the equation of the normal is :
y = mx - 2am - am3
Point of Contact are as follows :
P (am2, -2am)
Q (2a + am2, 0)
So, the area of the △PFQ :
\(=\frac{1}{2}\times|a+am^2||-2am|\)
120 = a2(1 + m2)m
so, a = 2, m = 3
So, only the option (A) satisfies the equation.
So, the correct option is (A) : (2, 3).
Top Questions on Conic sections
- Consider the ellipse \(\frac{x^2}{9}+\frac{y^2}{4}=1\). Let S (p, q) be a point in the first quadrant such that \(\frac{p^2}{9}+\frac{q^2}{4}>1\). Two tangents are drawn from S to the ellipse, of which one meets the ellipse at one end point of the minor axis and the other meets the ellipse at a point T in the fourth quadrant. Let R be the vertex of the ellipse with positive x-coordinate and Obe the center of the ellipse. If the area of the triangle △ORT is \(\frac{3}{2}\) , then which of the following options is correct ?
- JEE Advanced - 2024
- Mathematics
- Conic sections
- A normal with slope \(\frac{1}{\sqrt6}\) is drawn from the point (0, -α) to the parabola x2 = -4αy, where a > 0. Let L be the line passing through (0, -α) and parallel to the directrix of the parabola. Suppose that L intersects the parabola at two points A and B. Let r denote the length of the latus rectum and s denote the square of the length of the line segment AB. If r : s = 1 : 16 then the value of 24a is __________.
- JEE Advanced - 2024
- Mathematics
- Conic sections
- A particle moves along the curve \(\frac{x^2}{16}+\frac{y^2}{4}=1\). When the rate of change of abscissa is 4 times that of its ordinate, then the quadrant in which the particle lies is
- KCET - 2023
- Mathematics
- Conic sections
- The equations of two sides of a variable triangle are $x-0$ and $y=3$, and its third side is a tangent to the parabola $y^2=6 x$. The locus of its circumcentre is:
- JEE Main - 2023
- Mathematics
- Conic sections
- Let T1 and T2 be two distinct common tangents to the ellipse \(E: \frac{x^2}{6} + \frac{y^2}{3} = 1\) and the parabola \(P: y^2 = 12x\). Suppose that the tangent T1 touches P and E at the points A1 and A2, respectively and the tangent T2 touches P and E at the points A4 and A3, respectively. Then which of the following statements is(are) true?
- JEE Advanced - 2023
- Mathematics
- Conic sections
Questions Asked in JEE Advanced exam
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
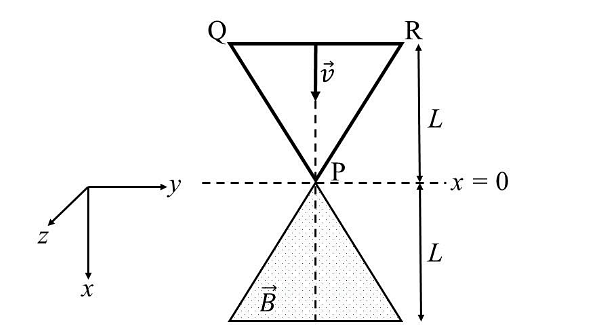
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0? - Two beads, each with charge q and mass m, are on a horizontal, frictionless, non-conducting, circular hoop of radius R. One of the beads is glued to the hoop at some point, while the other one performs small oscillations about its equilibrium position along the hoop. The square of the angular frequency of the small oscillations is given by [ \(\epsilon_0 \)is the permittivity of free space.]
- JEE Advanced - 2024
- Moving charges and magnetism
- A group of 9 students, s1, s2,…., s9, is to be divided to form three teams X, Y and Z of sizes 2, 3, and 4, respectively. Suppose that s1 cannot be selected for the team X and s2 cannot be selected for the team Y. Then the number of ways to form such teams, is _______.
- JEE Advanced - 2024
- Combinations
- Let \(\vec{p}=2\hat{i}+\hat{j}+3\hat{k}\) and \(\vec{q}=\hat{i}-\hat{j}+\hat{k}\). If for some real numbers α, β and γ we have
\(15\hat{i}+10\hat{j}+6\hat{k}=α(2\vec{p}+\vec{q})+β(\vec{p}-2\vec{q})+γ(\vec{p}\times\vec{q})\),
then the value of γ is ________.- JEE Advanced - 2024
- Vector Algebra
- Let X be a random variable, and let P(X = x) denote the probability that X takes the value x. Suppose that the points (x, P(X = x)), x = 0,1,2,3,4, lie on a fixed straight line in the xy -plane, and P(X = x) = 0 for all x ∈ R - {0,1,2,3,4}. If the mean of X is \(\frac{5}{2}\) , and the variance of X is α, then the value of 24α is ______.
- JEE Advanced - 2024
- Probability
Concepts Used:
Conic Sections
When a plane intersects a cone in multiple sections, several types of curves are obtained. These curves can be a circle, an ellipse, a parabola, and a hyperbola. When a plane cuts the cone other than the vertex then the following situations may occur:
Let ‘β’ is the angle made by the plane with the vertical axis of the cone
- When β = 90°, we say the section is a circle
- When α < β < 90°, then the section is an ellipse
- When α = β; then the section is said to as a parabola
- When 0 ≤ β < α; then the section is said to as a hyperbola
Read More: Conic Sections



