Question:
Let l1 be the line in xy-plane with x and y intercepts ⅛ and \(\frac{1}{4√2} \) respectively and l2 be the line in zx-plane with x and z intercepts -⅛ and \(−\frac{1}{6√3}\) respectively. If d is the shortest distance between the line l1 and l2, then d–2 is equal to ______.
Let l1 be the line in xy-plane with x and y intercepts ⅛ and \(\frac{1}{4√2} \) respectively and l2 be the line in zx-plane with x and z intercepts -⅛ and \(−\frac{1}{6√3}\) respectively. If d is the shortest distance between the line l1 and l2, then d–2 is equal to ______.
Updated On: Sep 24, 2024
Hide Solution
Verified By Collegedunia
Correct Answer: 51
Solution and Explanation
The correct answer is: 51.
\(\frac{x-\frac{1}{8}}{\frac{1}{8}}=\frac{y}{-\frac{1}{4\sqrt2}}=\frac{z}{0}....L_1\)
or
\(\frac{x-\frac{1}{8}}{1}=\frac{y}{-\sqrt2}=\frac{z}{0}....(i)\)
\(=\frac{\sqrt2}{\sqrt{32+16+54}}=\frac{!}{\sqrt51}\)
d–2 = 51
Was this answer helpful?
0
0
Top Questions on Plane
- Let R be the relation "is congruent to" on the set of all triangles in a plane. Is R:
- Let the acute angle bisector of the two planes \( x - 2y - 2z + 1 = 0 \) and \( 2x - 3y - 6z + 1 = 0 \) be the plane \( P \). Then which of the following points lies on \( P \)?
- Let the foot of perpendicular from a point \( P(1,2,-1) \) to the straight line \( L : \frac{x}{1} = \frac{y}{0} = \frac{z}{-1} \) be \( N \). Let a line be drawn from \( P \) parallel to the plane \( x + y + 2z = 0 \) which meets \( L \) at point \( Q \). If \( \alpha \) is the acute angle between the lines \( PN \) and \( PQ \), then \( \cos \alpha \) is equal to:
- If the plane \[ x - y + z + 4 = 0 \] divides the line joining the points \[ P(2,3,-1) \quad {and} \quad Q(1,4,-2) \] in the ratio \( l:m \), then \( l + m \) is:
- The equation of the plane passing through the point \( (1, 1, 1) \) and perpendicular to the planes \( 2x + y - 2z = 5 \) and \( 3x - 6y - 2z = 7 \) is:
View More Questions
Questions Asked in JEE Main exam
- The velocity-time graph of an object moving along a straight line is shown in the figure. What is the distance covered by the object between \( t = 0 \) to \( t = 4s \)?

- JEE Main - 2025
- Motion in a Straight Line
- The mass of magnesium required to produce 220 mL of hydrogen gas at STP on reaction with excess of dilute HCl is: (Given molar mass of Mg = 24 g/mol)
- JEE Main - 2025
- Gas laws
- 2.8 \( \times 10^{-3} \) mol of \( \text{CO}_2 \) is left after removing \( 10^{21} \) molecules from its ‘\( x \)’ mg sample. The mass of \( \text{CO}_2 \) taken initially is: Given: \( N_A = 6.02 \times 10^{23} \, \text{mol}^{-1} \)
- JEE Main - 2025
- Mole concept and Molar Masses
- Let \( \langle a_n \rangle \) be a sequence such that \( a_0 = 0 \), \( a_1 = \frac{1}{2} \), and \( 2a_{n+2} = 5a_{n+1} - 3a_n \).n= 0,1,2,3.... Then \( \sum_{k=1}^{100} a_k \) is equal to:
- JEE Main - 2025
- Sequences and Series
- Number of functions \( f: \{1, 2, \dots, 100\} \to \{0, 1\} \), that assign 1 to exactly one of the positive integers less than or equal to 98, is equal to:
- JEE Main - 2025
- Vectors
View More Questions
Concepts Used:
Distance of a Point from a Plane
The shortest perpendicular distance from the point to the given plane is the distance between point and plane. In simple terms, the shortest distance from a point to a plane is the length of the perpendicular parallel to the normal vector dropped from the particular point to the particular plane. Let's see the formula for the distance between point and plane.
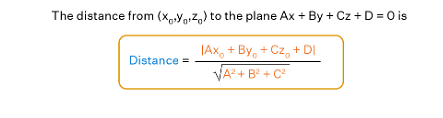
Read More: Distance Between Two Points