Let . If , then is:
The Correct Option is A
Solution and Explanation
Given:We have to find the value of if Consider:After comparing, we get....(i)....(ii)Adding equation (i) and (ii)Hence, the correct option is (A).
Top Questions on Transpose of a Matrix
- Let B =\(\begin{bmatrix} 1 & 3 & α \\ 1 & 2& 3 \\ α & α & 4 \end{bmatrix}\) , α>2 be the adjoint of a matrix A and |A| = 2, then [α - 2α α] B\(\begin{bmatrix} α \\ -2α \\ α \end{bmatrix}\)is equal to
- JEE Main - 2023
- Mathematics
- Transpose of a Matrix
- Let P be a square matrix such that P2 = I – P. For α, β, γ, δ ∈ N, if Pα + Pβ = γI – 29P and Pα – Pβ = δI – 13P, then α + β + γ – δ is equal to
- JEE Main - 2023
- Mathematics
- Transpose of a Matrix
- Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R.
Assertion A : For matrix A =\(\begin{bmatrix} 1 & 2 \\ 8 & 16 \end{bmatrix}\),rank of A = r(A) = 1
Reason R: For matrix A if |A| = 0, then it implies that rank of matrix A given by r(A) is less than full rank.
In the light of the above statements, choose the most appropriate answer from the options given below:- CUET (PG) - 2023
- Mathematics
- Transpose of a Matrix
- if A=\(\frac{1}{5! 6! 7!}\begin{bmatrix} 5! & 6! & 7!\\ 6! & 7! & 8! \\ 7! & 8! & 9! \end{bmatrix}\), then |adj(adj(2A))| is equal t
- JEE Main - 2023
- Mathematics
- Transpose of a Matrix
- Let Dk=\(\begin{vmatrix} 1 & 2k & 2k-1\\ n & n^2+n+2 & n^2 \\ n & n^2+n & n^2+n+2 \end{vmatrix} \) If \(∑^n_{k=1} D_k=96,\) The n is equal to
- JEE Main - 2023
- Mathematics
- Transpose of a Matrix
Questions Asked in JEE Main exam
- Let \[\vec{a} = \hat{i} + \hat{j} + \hat{k}, \quad \vec{b} = -\hat{i} - 8\hat{j} + 2\hat{k}, \quad \text{and} \quad \vec{c} = 4\hat{i} + c_2\hat{j} + c_3\hat{k} \]be three vectors such that \[\vec{b} \times \vec{a} = \vec{c} \times \vec{a}.\]If the angle between the vector $\vec{c}$ and the vector $3\hat{i} + 4\hat{j} + \hat{k}$ is $\theta$, then the greatest integer less than or equal to $\tan^2 \theta$ is:
- JEE Main - 2024
- Vector Algebra
- 10 mL of gaseous hydrocarbon on combustion gives 40 mL of CO\(_2\)(g) and 50 mL of water vapour. The total number of carbon and hydrogen atoms in the hydrocarbon is ______ .
- JEE Main - 2024
- Hydrocarbons
- If each term of a geometric progression \( a_1, a_2, a_3, \dots \) with \( a_1 = \frac{1}{8} \) and \( a_2 \neq a_1 \), is the arithmetic mean of the next two terms and \( S_n = a_1 + a_2 + \dots + a_n \), then \( S_{20} - S_{18} \) is equal to
- JEE Main - 2024
- Arithmetic Mean
A body of mass 1000 kg is moving horizontally with a velocity of 6 m/s. If 200 kg extra mass is added, the final velocity (in m/s) is:
- JEE Main - 2024
- speed and velocity
- $\textbf{Choose the correct statements about the hydrides of group 15 elements.}$
A. The stability of the hydrides decreases in the order \(\text{NH}_3 > \text{PH}_3 > \text{AsH}_3 > \text{SbH}_3 > \text{BiH}_3\)
B. The reducing ability of the hydrides increases in the order \(\text{NH}_3 < \text{PH}_3 < \text{AsH}_3 < \text{SbH}_3 < \text{BiH}_3\)
C. Among the hydrides, \(\text{NH}_3\) is a strong reducing agent while \(\text{BiH}_3\) is a mild reducing agent.
D. The basicity of the hydrides increases in the order \(\text{NH}_3 < \text{PH}_3 < \text{AsH}_3 < \text{SbH}_3 < \text{BiH}_3\)
Choose the most appropriate from the option given below:- JEE Main - 2024
- p -Block Elements
Concepts Used:
Transpose of a Matrix
The matrix acquired by interchanging the rows and columns of the parent matrix is called the Transpose matrix. The transpose matrix is also defined as - “A Matrix which is formed by transposing all the rows of a given matrix into columns and vice-versa.”
The transpose matrix of A is represented by A’. It can be better understood by the given example:

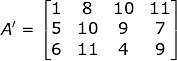
Now, in Matrix A, the number of rows was 4 and the number of columns was 3 but, on taking the transpose of A we acquired A’ having 3 rows and 4 columns. Consequently, the vertical Matrix gets converted into Horizontal Matrix.
Hence, we can say if the matrix before transposing was a vertical matrix, it will be transposed to a horizontal matrix and vice-versa.
Read More: Transpose of a Matrix



