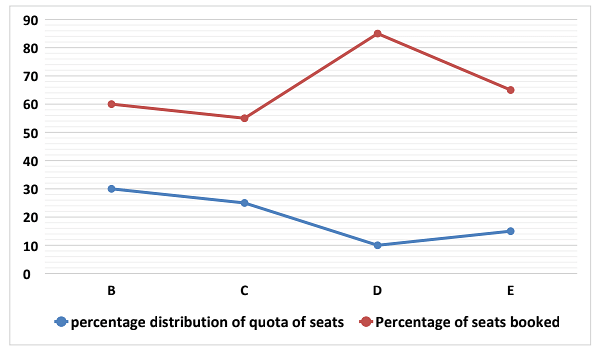
A train ‘T’ starts from station ‘A’ for station ‘F’. In between stations ‘A’ and ‘F’, there are four intermediate stations ‘B’, ‘C’, ‘D’ and ‘E’, respectively, in the same order. Stations ‘A’, ‘B’, ‘C’, ‘D’ and ‘E’ has quota for seats booking. The line graph given below represents the percentage distribution of quota of seats given to the respective stations out of total number of seats in the train and percentage of seats booked out of them.
The table below represents the total vacant seats in the train after leaving the respective stations.
| Stations | Total vacant seats |
| B | 562 |
| C | 494 |
| D | 514 |
| E | 472 |
Note:
1. When train left station A, number of vacant seats was 688 and 30% of quota seats of station A were not booked.
2. A seat can be booked for only one person from the respective stations and the same person can board the train from that station.
3. All the persons who booked tickets boarded the train.
Find the ratio of number of passengers who boarded the train at station ‘B’ and number of passengers who de-boarded the train at station ‘D’.
- 13:9
- 12:7
- 18:11
- 10:3
The Correct Option is C
Solution and Explanation
The correct option is (C): 18:11.
Let total number of seats in the train be ‘x’
Percentage of quota of seats given to station ‘A’ = 100 – (30 + 25 + 10 +15) = 20%
So, number of seats available for booking in station A = 0.2x
Therefore, number of seats booked station A = 70% of 0.2x = 0.14x
So, x – 688 = 0.14x
Or, 0.86x = 688
Or, x = 688/0.86 = 800
The table below shows the information about number of seats available, booked and not booked for respective stations.
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 20% of 800 = 160 | 70% of 160 =112 | 48 |
| B | 30% of 800 = 240 | 60% of 240 =144 | 96 |
| C | 25% of 800 = 200 | 55% of 200 =110 | 90 |
| D | 10% of 800 = 80 | 85% of 80 = 68 | 12 |
| E | 15% of 800 = 120 | 65% of 120 =78 | 42 |
So, number of passengers in the train after leaving station ‘B’ = 800 –562 = 238
Number of passengers who boarded from station ‘A’ = 112
Number of passengers who boarded from station ‘B’ = 144
Therefore, number of passengers in the train after leaving station ‘B’ =Number of passengers who boarded from station ‘A’ + Number of
passengers who boarded from station ‘B’ – number of passengers who de-boarded at station ‘B’
So, 238 = 112 + 144 – number of passengers who de-boarded at station ‘B’
Or, number of passengers who de-boarded at station ‘B’ = 256 – 238 =18
Similarly,
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 112 | 112 | - |
| B | 144 | 238 | 18 |
| C | 110 | 306 | 42 |
| D | 68 | 286 | 88 |
| E | 78 | 328 | 36 |
| F | - | - | 328 |
Required ratio = 144:88 = 18:11.
boarded at station ‘B’
So, 238 = 112 + 144 – number of passengers who de-boarded at station ‘B’
Or, number of passengers who de-boarded at station ‘B’ = 256 – 238 =18
Similarly,
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 112 | 112 | - |
| B | 144 | 238 | 18 |
| C | 110 | 306 | 42 |
| D | 68 | 286 | 88 |
| E | 78 | 328 | 36 |
| F | - | - | 328 |
Required ratio = 144:88 = 18:11.
Out of total number of passengers in the train after it left station ‘C’, 50% were females. Find the difference between number of males in the train after it left station ‘C’ and number of passengers who deboarded the train at station ‘B’.
- 135
- 215
- 123
- 141
The Correct Option is A
Solution and Explanation
The correct option is (A): 135.
Let total number of seats in the train be ‘x’
Percentage of quota of seats given to station ‘A’ = 100 – (30 + 25 + 10 +15) = 20%
So, number of seats available for booking in station A = 0.2x
Therefore, number of seats booked station A = 70% of 0.2x = 0.14x
So, x – 688 = 0.14x
Or, 0.86x = 688
Or, x = \(\frac{688}{0.86} \)= 800
The table below shows the information about number of seats available, booked and not booked for respective stations.
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 20% of 800 = 160 | 70% of 160 =112 | 48 |
| B | 30% of 800 = 240 | 60% of 240 =144 | 96 |
| C | 25% of 800 = 200 | 55% of 200 =110 | 90 |
| D | 10% of 800 = 80 | 85% of 80 = 68 | 12 |
| E | 15% of 800 = 120 | 65% of 120 =78 | 42 |
So, number of passengers in the train after leaving station ‘B’ = 800 –562 = 238
Number of passengers who boarded from station ‘A’ = 112
Number of passengers who boarded from station ‘B’ = 144
Therefore, number of passengers in the train after leaving station ‘B’ =Number of passengers who boarded from station ‘A’ + Number of
passengers who boarded from station ‘B’ – number of passengers who de-boarded at station ‘B’
So, 238 = 112 + 144 – number of passengers who de-boarded at station ‘B’
Or, number of passengers who de-boarded at station ‘B’ = 256 – 238 =18
Similarly,
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 112 | 112 | - |
| B | 144 | 238 | 18 |
| C | 110 | 306 | 42 |
| D | 68 | 286 | 88 |
| E | 78 | 328 | 36 |
| F | - | - | 328 |
Required difference = (0.5 × 306) – 18 = 153 – 18 = 135.
rded at station ‘B’
So, 238 = 112 + 144 – number of passengers who de-boarded at station ‘B’
Or, number of passengers who de-boarded at station ‘B’ = 256 – 238 =18
Similarly,
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 112 | 112 | - |
| B | 144 | 238 | 18 |
| C | 110 | 306 | 42 |
| D | 68 | 286 | 88 |
| E | 78 | 328 | 36 |
| F | - | - | 328 |
Required difference = (0.5 × 306) – 18 = 153 – 18 = 135.
Find the average of the number of passengers who de-boarded the train at stations ‘E’ and ‘F’ together.
- 212
- 272
- 192
- 182
The Correct Option is D
Solution and Explanation
The correct option is (D): 182.
Let total number of seats in the train be ‘x’
Percentage of quota of seats given to station ‘A’ = 100 – (30 + 25 + 10 +15) = 20%
So, number of seats available for booking in station A = 0.2x
Therefore, number of seats booked station A = 70% of 0.2x = 0.14x
So, x – 688 = 0.14x
Or, 0.86x = 688
Or, x = 688/0.86 = 800
The table below shows the information about number of seats available, booked and not booked for respective stations.
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 20% of 800 = 160 | 70% of 160 =112 | 48 |
| B | 30% of 800 = 240 | 60% of 240 =144 | 96 |
| C | 25% of 800 = 200 | 55% of 200 =110 | 90 |
| D | 10% of 800 = 80 | 85% of 80 = 68 | 12 |
| E | 15% of 800 = 120 | 65% of 120 =78 | 42 |
So, number of passengers in the train after leaving station ‘B’ = 800 –562 = 238
Number of passengers who boarded from station ‘A’ = 112
Number of passengers who boarded from station ‘B’ = 144
Therefore, number of passengers in the train after leaving station ‘B’ =Number of passengers who boarded from station ‘A’ + Number of
passengers who boarded from station ‘B’ – number of passengers who de-boarded at station ‘B’
So, 238 = 112 + 144 – number of passengers who de-boarded at station ‘B’
Or, number of passengers who de-boarded at station ‘B’ = 256 – 238 =18
Similarly,
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 112 | 112 | - |
| B | 144 | 238 | 18 |
| C | 110 | 306 | 42 |
| D | 68 | 286 | 88 |
| E | 78 | 328 | 36 |
| F | - | - | 328 |
Required average = {\(\frac{(36 + 328)}{2}\)} = 182.
After the train left station ‘D’, each passenger has 3 bags with him.
Find the total number of bags with the passengers in the train after it left
station ‘D’.
Find the total number of bags with the passengers in the train after it left
station ‘D’.
- 766
- 512
- 858
- 912
The Correct Option is C
Solution and Explanation
The correct option is (C): 858.
Let total number of seats in the train be ‘x’
Percentage of quota of seats given to station ‘A’ = 100 – (30 + 25 + 10 +15) = 20%
So, number of seats available for booking in station A = 0.2x
Therefore, number of seats booked station A = 70% of 0.2x = 0.14x
So, x – 688 = 0.14x
Or, 0.86x = 688
Or, x = 688/0.86 = 800
The table below shows the information about number of seats available, booked and not booked for respective stations.
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 20% of 800 = 160 | 70% of 160 =112 | 48 |
| B | 30% of 800 = 240 | 60% of 240 =144 | 96 |
| C | 25% of 800 = 200 | 55% of 200 =110 | 90 |
| D | 10% of 800 = 80 | 85% of 80 = 68 | 12 |
| E | 15% of 800 = 120 | 65% of 120 =78 | 42 |
So, number of passengers in the train after leaving station ‘B’ = 800 –562 = 238
Number of passengers who boarded from station ‘A’ = 112
Number of passengers who boarded from station ‘B’ = 144
Therefore, number of passengers in the train after leaving station ‘B’ =Number of passengers who boarded from station ‘A’ + Number of
passengers who boarded from station ‘B’ – number of passengers who de-boarded at station ‘B’
So, 238 = 112 + 144 – number of passengers who de-boarded at station ‘B’
Or, number of passengers who de-boarded at station ‘B’ = 256 – 238 =18
Similarly,
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 112 | 112 | - |
| B | 144 | 238 | 18 |
| C | 110 | 306 | 42 |
| D | 68 | 286 | 88 |
| E | 78 | 328 | 36 |
| F | - | - | 328 |
Required number of bags = 286 × 3 = 858.
If at each station, 75% of total number of passengers who boarded the train were males then find the sum of number of all the females who boarded the train at given stations.
- 194
- 148
- 156
- 128
The Correct Option is D
Solution and Explanation
The correct option is (D): 128.
Let total number of seats in the train be ‘x’
Percentage of quota of seats given to station ‘A’ = 100 – (30 + 25 + 10 +15) = 20%
So, number of seats available for booking in station A = 0.2x
Therefore, number of seats booked station A = 70% of 0.2x = 0.14x
So, x – 688 = 0.14x
Or, 0.86x = 688
Or, x = 688/0.86 = 800
The table below shows the information about number of seats available, booked and not booked for respective stations.
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 20% of 800 = 160 | 70% of 160 =112 | 48 |
| B | 30% of 800 = 240 | 60% of 240 =144 | 96 |
| C | 25% of 800 = 200 | 55% of 200 =110 | 90 |
| D | 10% of 800 = 80 | 85% of 80 = 68 | 12 |
| E | 15% of 800 = 120 | 65% of 120 =78 | 42 |
So, number of passengers in the train after leaving station ‘B’ = 800 –562 = 238
Number of passengers who boarded from station ‘A’ = 112
Number of passengers who boarded from station ‘B’ = 144
Therefore, number of passengers in the train after leaving station ‘B’ =Number of passengers who boarded from station ‘A’ + Number of
passengers who boarded from station ‘B’ – number of passengers who de-boarded at station ‘B’
So, 238 = 112 + 144 – number of passengers who de-boarded at station ‘B’
Or, number of passengers who de-boarded at station ‘B’ = 256 – 238 =18
Similarly,
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 112 | 112 | - |
| B | 144 | 238 | 18 |
| C | 110 | 306 | 42 |
| D | 68 | 286 | 88 |
| E | 78 | 328 | 36 |
| F | - | - | 328 |
Required number of females = 0.25 × (112 + 144 + 110 + 68 + 78) =128.
Top Questions on Data Interpretation
- Read the Passage carefully and answer the following questions.
An air conditioner (AC) unit has three operating modes: Eco, Normal, and Turbo. The power consumption in each mode is as follows: Eco mode consumes 1000 watts, Normal mode consumes 1200 watts, and Turbo mode consumes 1500 watts. Yesterday, the AC was in operation from 2 PM to 10 PM. From 2 PM to 6 PM it ran in Eco mode. From 6 PM to 8 PM, it ran in Normal mode. From 8 PM to 10 PM it ran in Turbo mode.- CAT - 2024
- Data Interpretation & Logical Reasoning (DILR)
- Data Interpretation
- Read the Passage carefully and answer the following questions
A health food store specializing in dietary supplements and whole grains recorded the following sales figures (in kilograms) for various food categories last month: Millets (M) = 500 kg at a cost price of 40/kg and selling price of 50/kg; Protein supplements (P) = 300 kg at a cost price of 80/kg and selling price of 100/kg; Vitamin supplements (V) = 200 kg at a cost price of 60/kg and selling price of 80/kg; Carbohydrates (C) = 600 kg at a cost price of 80/kg and selling price of 100/kg; Fats (F) = 100 kg at a cost price of 120/kg and selling price of 150/kg. Additionally, they sold 50 kg of mixed nuts (N) at a cost price of 100/kg and a selling price of 130/kg- CAT - 2024
- Data Interpretation & Logical Reasoning (DILR)
- Data Interpretation
- In a class of 40 students, the ratio of boys to girls is 3:2. The average marks scored by boys is 42, and that by girls is 46. What is the average marks scored by the whole class?
- CUET (UG) - 2024
- General Aptitude
- Data Interpretation
- Shown below is a cross-section of two different trees of same species and age but found in different locations. Based on the image, which of the statement(s) is/are TRUE.

- UCEED - 2024
- Logical Reasoning
- Data Interpretation
- In an election, the share of valid votes received by the four candidates A, B, C, and D is represented by the pie chart shown. The total number of votes cast in the election were 1,15,000, out of which 5,000 were invalid.
Based on the data provided, the total number of valid votes received by the candidates B and C is- GATE AR - 2024
- General Aptitude
- Data Interpretation
Questions Asked in CAT exam
- ABCD is a rectangle with sides AB = 56 cm and BC = 45 cm, and E is the midpoint of side CD. Then, the length, in cm, of radius of incircle of \(\triangle ADE\) is
- CAT - 2024
- Mensuration
- Let $x$ be a positive real number such that $4 \log_{10} x + 4 \log_{100} x + 8 \log_{1000} x = 13$ , then the greatest integer not exceeding $x$. is
- CAT - 2024
- Logarithms
- Two places A and B are 45 kms apart and connected by a straight road. Anil goes from A to B while Sunil goes from B to A. Starting at the same time, they cross each other in exactly 1 hour 30 minutes. If Anil reaches B exactly 1 hour 15 minutes after Sunil reaches A, the speed of Anil, in km per hour, is
- CAT - 2024
- Time Speed and Distance
- In the $XY$-plane, the area, in sq. units, of the region defined by the inequalities $y \ge x + 4$ and $-4 \le x^2 + y^2 + 4(x - y) \le 0$ is
- CAT - 2024
- Coordinate Geometry
- There are four numbers such that average of first two numbers is 1 more than the first number, average of first three numbers is 2 more than average of first two numbers, and average of first four numbers is 3 more than average of first three numbers. Then, the difference between the largest and the smallest numbers, is
- CAT - 2024
- Averages



