Select Goal &
City
Select Goal
Explore
Question:
Consider a vector field \( \vec{F} = (2xz + 3y^2)\hat{y} + 4yz^2\hat{z} \). The closed path (\( \Gamma \): \( A \rightarrow B \rightarrow C \rightarrow D \rightarrow A \)) in the \( z = 0 \) plane is shown in the figure.
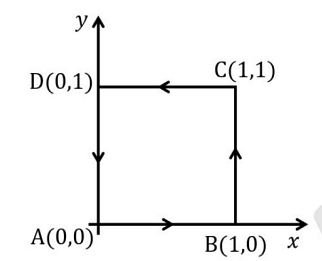
\( \oint_\Gamma \vec{F} \cdot d\vec{l} \) denotes the line integral of \( \vec{F} \) along the closed path \( \Gamma \). Which of the following options is/are true?
Consider a vector field \( \vec{F} = (2xz + 3y^2)\hat{y} + 4yz^2\hat{z} \). The closed path (\( \Gamma \): \( A \rightarrow B \rightarrow C \rightarrow D \rightarrow A \)) in the \( z = 0 \) plane is shown in the figure.
\( \oint_\Gamma \vec{F} \cdot d\vec{l} \) denotes the line integral of \( \vec{F} \) along the closed path \( \Gamma \). Which of the following options is/are true?
\( \oint_\Gamma \vec{F} \cdot d\vec{l} \) denotes the line integral of \( \vec{F} \) along the closed path \( \Gamma \). Which of the following options is/are true?
Updated On: Jul 12, 2024
- \( \oint_\Gamma \vec{F} \cdot d\vec{l} = 0 \)
- \( \vec{F} \) is non-conservative.
- \(\vec{\nabla} \cdot \vec{F} = 0\)
- \(\vec{F}\) can be written as the gradient of a scalar field
Hide Solution
Verified By Collegedunia
The Correct Option is A, B
Solution and Explanation
The correct Answers are (A):\( \oint_\Gamma \vec{F} \cdot d\vec{l} = 0 \),(B):\( \vec{F} \) is non-conservative.
Was this answer helpful?
0
0
Top Questions on Vectors
- The least positive integral value of \( \alpha \), for which the angle between the vectors \( \alpha \hat{i} - 2\hat{j} + 2\hat{k} \) and \( \alpha \hat{i} + 2\alpha \hat{j} - 2\hat{k} \) is acute, is ______.
- Let \(\vec{a} = \hat{i} + 2\hat{j} + \hat{k}\), \(\vec{b} = 3(\hat{i} - \hat{j} + \hat{k})\). Let \(\vec{c}\) be the vector such that \(\vec{a} \times \vec{c} = \vec{b}\) and \(\vec{a} \cdot \vec{c} = 3\). Then \(\vec{a} \cdot ((\vec{c} \times \vec{b}) - \vec{b} \cdot \vec{c})\) is equal to:
- Let \( A (2, 3, 5) \) and \( C(-3, 4, -2) \) be opposite vertices of a parallelogram \( ABCD \). If the diagonal \( \overrightarrow{BD} = \hat{i} + 2 \hat{j} + 3 \hat{k} \), then the area of the parallelogram is equal to
- Let \( \vec{a} = a_1 \hat{i} + a_2 \hat{j} + a_3 \hat{k} \) and \( \vec{b} = b_1 \hat{i} + b_2 \hat{j} + b_3 \hat{k} \) be two vectors such that \( |\vec{a}| = 1 \), \( \vec{a} \times \vec{b} = 2 \), and \( |\vec{b}| = 4 \). If \( \vec{c} = 2(\vec{a} \times \vec{b}) - 3\vec{b} \), then the angle between \( \vec{b} \) and \( \vec{c} \) is equal to:
- Given that \( A^\alpha \) and \( B_\beta \) (\(\alpha, \beta = 1, 2, 3, \ldots, n\)) are contravariant and covariant vectors, respectively, and by convention, any repeated indices are summed over. Which of the following expressions is/are tensors?
View More Questions
Questions Asked in GATE PH exam
- Two point charges of charge \( +q \) each are placed a distance \( 2d \) apart. A grounded solid conducting sphere of radius \( a \) is placed midway between them. Assume \( a^2 \ll d^2 \). Which of the following statements is/are true?
- GATE PH - 2024
- Electric Charge
- When an unpolarized plane electromagnetic wave in a dielectric medium with refractive index \( n_1 \) is incident on a plane interface separating it from another dielectric medium with refractive index \( n_2 \) (where \( n_2 > n_1 \)), and the angle of incidence is \(\tan^{-1} \left( \frac{n_2}{n_1} \right) \), the following statement is true:
- GATE PH - 2024
- Electromagnetic Waves
- Binding energy and rest mass energy of a two-nucleon bound state are denoted by \( B \) and \( mc^2 \), respectively, where \( c \) is the speed of light. The minimum energy of a photon required to dissociate the bound state is _______.
- If a thermodynamical system is adiabatically isolated and experiences a change in volume under an externally applied constant pressure, then the thermodynamical potential minimized at equilibrium is the
- GATE PH - 2024
- Thermodynamics
- The mean distance between the two atoms of an HD molecule is \( r \), where H and D denote hydrogen and deuterium, respectively. The mass of the hydrogen atom is \( m_H \). The energy difference between the two lowest lying rotational states of HD in multiples of \(\frac{h^2}{m_H r^2}\) is:
- GATE PH - 2024
- atom structure models
View More Questions
SUBSCRIBE TO OUR NEWS LETTER
COLLEGE NOTIFICATIONSEXAM NOTIFICATIONSNEWS UPDATES
Download the Collegedunia app on 
© 2024 Collegedunia Web Pvt. Ltd. All Rights Reserved