Select Goal &
City
Select Goal
Explore
Question:
ABC is an isosceles triangle with an inscribed circle with center O. Let P be the midpoint of BC. If AB=AC=15 and BC=10,then OP equals
ABC is an isosceles triangle with an inscribed circle with center O. Let P be the midpoint of BC. If AB=AC=15 and BC=10,then OP equals
Updated On: Jun 25, 2024
- \(\frac{\sqrt5}{\sqrt2}\) unit
\(\frac{5}{\sqrt2}\) unit
- \(\frac{2}{\sqrt5}\) unit
- \(5\sqrt2\) unit
Hide Solution
Verified By Collegedunia
The Correct Option is B
Approach Solution - 1
The correct answer is option (B) : \(\frac{5}{\sqrt2}\) unit.
Was this answer helpful?
6
24
Hide Solution
Verified By Collegedunia
Approach Solution -2
Geometric Solution Simplified
1. Draw a perpendicular line AD to BC.
2. D is the midpoint of BC, so BD = DC.
3. Given BC = 14 cm, then BD = DC = 7 cm.
4. Using the Pythagorean theorem in triangle ADB:
AB2 = AD2 + BD2
252 = AD2 + 72
625 = AD2 + 49
AD2 = 625 - 49 = 576
AD = 24 cm
5. Using the Pythagorean theorem in triangle ODB:
OB2 = OD2 + BD2
Here OD = AD - AO = 24 - r, where r is the radius of the circle:
(24 - r)2 + 72 = r2
(24 - r)2 + 49 = r2
Expanding and simplifying:
576 - 48r + r2 + 49 = r2
576 + 49 - 48r = 0
625 - 48r = 0
48r = 625
r = 625 / 48 ≈ 13.02 cm
1. Draw a perpendicular line AD to BC.
2. D is the midpoint of BC, so BD = DC.
3. Given BC = 14 cm, then BD = DC = 7 cm.
4. Using the Pythagorean theorem in triangle ADB:
AB2 = AD2 + BD2
252 = AD2 + 72
625 = AD2 + 49
AD2 = 625 - 49 = 576
AD = 24 cm
5. Using the Pythagorean theorem in triangle ODB:
OB2 = OD2 + BD2
Here OD = AD - AO = 24 - r, where r is the radius of the circle:
(24 - r)2 + 72 = r2
(24 - r)2 + 49 = r2
Expanding and simplifying:
576 - 48r + r2 + 49 = r2
576 + 49 - 48r = 0
625 - 48r = 0
48r = 625
r = 625 / 48 ≈ 13.02 cm
Was this answer helpful?
0
0
Top Questions on Three Dimensional Geometry
- A straight line drawn from the point P(1,3, 2), parallel to the line \(\frac{x-2}{1}=\frac{y-4}{2}=\frac{z-6}{1}\), intersects the plane L1 : x - y + 3z = 6 at the point Q. Another straight line which passes through Q and is perpendicular to the plane L1 intersects the plane L2 : 2x - y + z = -4 at the point R. Then which of the following statements is (are) TRUE ?
- JEE Advanced - 2024
- Mathematics
- Three Dimensional Geometry
- Let y ∈ R be such that the lines \(L_1:\frac{x+11}{1}=\frac{y+21}{2}=\frac{z+29}{3}\) and \(L_2:\frac{x+16}{3}=\frac{y+11}{2}=\frac{z+4}{\gamma}\) intersect. Let R1 be the point of intersection of L1 and L2. Let O = (0, 0 ,0), and \(\hat{n}\) denote a unit normal vector to the plane containing both the lines L1 and L2.
Match each entry in List-I to the correct entry in List-II.The correct option isList - I List - II (P) γ equals (1) \(-\hat{i}-\hat{j}+\hat{k}\) (Q) A possible choice for \(\hat{n}\) is (2) \(\sqrt{\frac{3}{2}}\) (R) \(\overrightarrow{OR_1}\) equals (3) 1 (S) A possible value of \(\overrightarrow{OR_1}.\hat{n}\) is (4) \(\frac{1}{\sqrt6}\hat{i}-\frac{2}{\sqrt6}\hat{j}+\frac{1}{\sqrt6}\hat{k}\) (5) \(\sqrt{\frac{2}{3}}\) - JEE Advanced - 2024
- Mathematics
- Three Dimensional Geometry
- Let R3 denote the three-dimensional space. Take two points P = (1, 2, 3) and Q = (4, 2 ,7). Let
dist(X, Y) denote the distance between two points X and Y in R3. Let
\(S=\left\{X\in\R^3:(dist(X,P)^2)-(dist(X,Q))^2=50\right\}\ and\)
\(T=\left\{Y\in \R^3:(dist(Y,Q))^2-(dist(Y,P))^2=50\right\}\)
Then which of the following statements is (are) TRUE ?- JEE Advanced - 2024
- Mathematics
- Three Dimensional Geometry
- If the foot is perpendicular from (1, 2, 3) to the line \(\frac{x+1}{2} = \frac{y-2}{5} = \frac{z-1}{1}\) is \(( a, \beta, \gamma)\), then find \(a + \beta + \gamma\)
- JEE Main - 2024
- Mathematics
- Three Dimensional Geometry
- Let the line / : x = \(\frac{1-y}{2}=\frac{z-3}{\lambda}, \lambda \in R\) meet the plane P : x+2y +3z = 4 at the point \((\alpha, \beta, \lambda)\). If the angle between the line I and the plane P is \(cos^{-1}\bigg(\sqrt{\frac{5}{14}}\bigg)\) then \(\alpha+2\beta+6\lambda\) is equal to______.
- JEE Main - 2023
- Mathematics
- Three Dimensional Geometry
View More Questions
Questions Asked in WBJEE exam
- Three identical convex lenses each of focal length f are placed in a straight line separated by a distance f from each other. An object is located in \(\frac{f}{2}\) in front of the leftmost lens. Then,
- WBJEE - 2023
- Ray optics and optical instruments
- \(\lim_{x\rightarrow \infty}\){\(x-\sqrt[n]{(x-a_1)(x-a_2)......(x-a_n)}\)} where a1,a2,.....an are positive rational numbers.The limit
- A particle of mass m is projected at velocity at a velocity u, making an angle θ with the horizontal(x-axis). If the angle of projection θ is varied keeping all other parameters same, then magnitude of angular momentum(L) at its maximum height about the point of projection varies with θ as,
- WBJEE - 2023
- System of Particles & Rotational Motion
- If \(\int \frac{dx}{(x+1)(x-2)(x-3)}=\frac{1}{k}log_e\left \{ \frac{|x-3|^3|x+1|}{(x-2)^4}\right \}+c\), then the value of k is
- WBJEE - 2023
- Integrals of Some Particular Functions
- A rectangle ABCD has its side parallel to the line y=2x and vertices A,B,D are on y=1,x=1 and x=-1 respectively. The coordinate of C can be
- WBJEE - 2023
- Straight lines
View More Questions
Concepts Used:
Three Dimensional Geometry
Mathematically, Geometry is one of the most important topics. The concepts of Geometry are derived w.r.t. the planes. So, Geometry is divided into three major categories based on its dimensions which are one-dimensional geometry, two-dimensional geometry, and three-dimensional geometry.
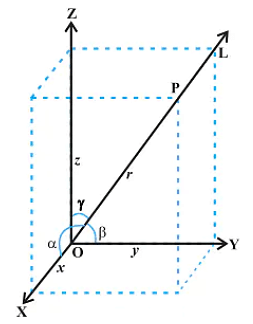
Direction Cosines and Direction Ratios of Line:
Consider a line L that is passing through the three-dimensional plane. Now, x,y and z are the axes of the plane and α,β, and γ are the three angles the line makes with these axes. These are commonly known as the direction angles of the plane. So, appropriately, we can say that cosα, cosβ, and cosγ are the direction cosines of the given line L.
SUBSCRIBE TO OUR NEWS LETTER
COLLEGE NOTIFICATIONSEXAM NOTIFICATIONSNEWS UPDATES
Download the Collegedunia app on 
© 2024 Collegedunia Web Pvt. Ltd. All Rights Reserved