Question:
A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
Updated On: Nov 2, 2023
Hide Solution
Verified By Collegedunia
Solution and Explanation

Let AB be the statue, BC be the pedestal, and D be the point on the ground from where the elevation angles are to be measured.
In ∆BCD,
\(\frac{BC}{CD} = tan 45°\)
\(\frac{BC}{ CD} = 1 \)
\(BC = CD\)
In ∆ACD,
\(\frac{AB + BC}{ BC} = tan 60°\)
\(\frac{AB + BC }{ BC} = \sqrt3\)
\(1.6 + BC = BC \sqrt3\)
\(BC = (\sqrt3 -1) = 1.6\)
\(BC =\frac{ (1.6) (\sqrt3 +1)}{ (\sqrt3 -1) (\sqrt3+ 1)}\)
\(BC = \frac{1.6 (\sqrt3+1)}{ (\sqrt3)^2 - (1)^2}\)
\(BC = \frac{1.6 (\sqrt3 +1)}2 = 0.8\, (\sqrt3 +1)\)
Therefore, the height of the pedestal is\(0.8\, (\sqrt3 +1)\) m.
Was this answer helpful?
0
0
Top Questions on Heights and Distances
- If two towers of heights h1, and h2 subtend angles of 30° and 60° respectively at the midpoint of the line joining their feet, then the ratio of h1: h2 is
- AP POLYCET - 2024
- Mathematics
- Heights and Distances
- A tree is broken by wind, its upper part touches the ground at a point 10 metre from the foot of the tree and makes an angle of 45° with the ground. Then what is the entire height of the tree?
- AP POLYCET - 2024
- Mathematics
- Heights and Distances
- A man standing on the bank of a river observes that the angle subtended by a tree standing on the opposite bank is 60° on his side of Bank. When he moved away 24 m from the bank, he finds the angle to be 30°. Find the breadth of the river:
- CUET (UG) - 2023
- Mathematics
- Heights and Distances
- A ladder of length 30 m is leaning against a wall making an angle of 30° with the horizontal. Find the distance between the foot of the ladder and the wall.
- CUET (UG) - 2023
- Mathematics
- Heights and Distances
- The base of a tower is 80m away from a point A on the ground. If the angle of elevation of the top of the tower from A is 45. Calculate the height of the tower.
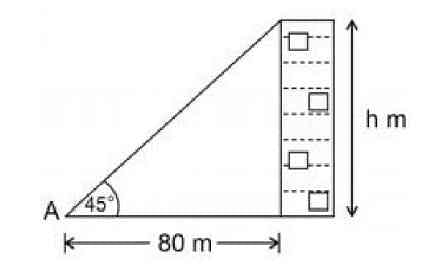
- CUET (PG) - 2023
- Mathematics
- Heights and Distances
View More Questions
Questions Asked in CBSE X exam
- Why are books referred to as a man’s best companion? Which is your favourite book and why? Write a paragraph about that book.
- CBSE X
- The Book That Saved The Earth
- Does Bholi enjoy her first day at school?
- CBSE X
- Bholi
- Draw the structure of a neuron and explain its function.
- CBSE X
- Animals – Nervous System
- Show how you would connect three resistors, each of resistance 6 Ω, so that the combination has a resistance of
- 9 Ω
- 4 Ω
- CBSE X
- Resistance Of A System Of Resistors
- Bholi’s real name is Sulekha. We are told this right at the beginning. But only in the last but one paragraph of the story is Bholi called Sulekha again. Why do you think she is called Sulekha at that point in the story?
- CBSE X
- Bholi
View More Questions



