A disk of radius $R$ with uniform positive charge density $\sigma$ is placed on the $x y$ plane with its center at the origin. The Coulomb potential along the $z$-axis is $V(z)=\frac{\sigma}{2 \epsilon_0}\left(\sqrt{R^2+z^2}-z\right)$.
A particle of positive charge $q$ is placed initially at rest at a point on the $z$ axis with $z=z_0$ and $z_0>0$. In addition to the Coulomb force, the particle experiences a vertical force $\vec{F}=-c \hat{k}$ with $c>0$ Let $\beta=\frac{2 c \in_0}{q \sigma}$. Which of the following statement(s) is(are) correct?
A particle of positive charge $q$ is placed initially at rest at a point on the $z$ axis with $z=z_0$ and $z_0>0$. In addition to the Coulomb force, the particle experiences a vertical force $\vec{F}=-c \hat{k}$ with $c>0$ Let $\beta=\frac{2 c \in_0}{q \sigma}$. Which of the following statement(s) is(are) correct?
- For $\beta=\frac{1}{4}$ and $z_0=\frac{25}{7} R$, the particle reaches the origin.
- For $\beta=\frac{1}{4}$ and $z_0=\frac{3}{7} R$, the particle reaches the origin.
- For $\beta=\frac{1}{4}$ and $z_0=\frac{R}{\sqrt{3}}$, the particle returns back to $z=z_0$.
- For $\beta>1$ and $z_0>0$, the particle always reaches the origin.
The Correct Option is A, C, D
Solution and Explanation
Given:
\(F_1 = \frac{26\sqrt{R^2 + Z^2}}{2E_0}\)
\(F_2 = -ck\)
\(\frac{\alpha \sigma}{280}\)
For equilibrium at \(z = \frac{Z}{o}\)
\(F_1 = F_2\)
\(\frac{\alpha \sigma}{280} \cdot \frac{Z}{\sqrt{R^2 + Z^2}} = c\)
From equation (1):
\(c = (1 - 3\frac{Z}{\sqrt{R^2 + Z^2}})\)
\(\frac{Z}{\sqrt{R^2 + Z^2}} = c(1 - 3\frac{Z}{\sqrt{R^2 + Z^2}})\)
\(\frac{1}{4} \cdot \frac{Z}{\sqrt{R^2 + Z^2}} = \frac{4c}{2c_{80}}\)
\(\frac{7}{\sqrt{R} - R} = 1.13R\)
\(𝑍>1.13𝑅⇒𝐹_2>𝐹_1\) Particle reaches the origin.
\(𝑍<1.13𝑅⇒𝐹_1>𝐹_2\) Particle reaches back to 𝑧=𝑍𝑜
Top Questions on Electric Flux
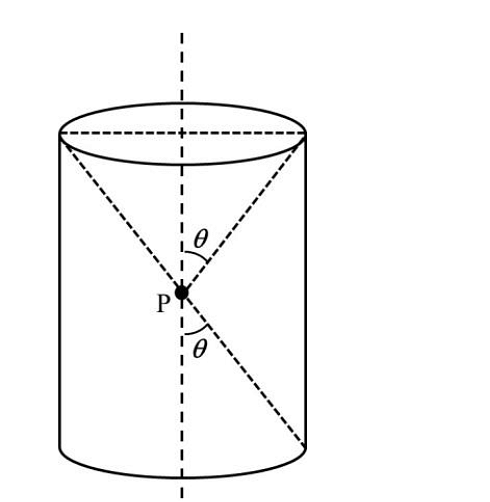
- A charge is kept at the central point P of a cylindrical region. The two edges subtend a half-angle \(\theta\) at P, as shown in the figure. When \(\theta = 30\) , then the electric flux through the curved surface of the cylinder is \(Φ\). If \(\theta= 60\degree\) , then the electric flux through the curved surface becomes \(Φ/√𝑛\), where the value of n is______.
- JEE Advanced - 2024
- Physics
- Electric Flux
Expression for an electric field is given by $\overrightarrow{ E }=4000 x^2 i \frac{ V }{ m }$ The electric flux through the cube of side $20 cm$ when placed in electric field (as shown in the figure) is ___$V cm$

- JEE Main - 2023
- Physics
- Electric Flux
- A capacitor of capacitance C is charged to a potential V. The flux of the electric field through a closed surface enclosing the positive plate of the capacitor is :
- JEE Main - 2023
- Physics
- Electric Flux
- In a cuboid of dimension \(2L \times 2L \times L\), a charge q is placed at the center of the surface ‘S’ having area of 4 L2. The flux through the opposite surface to ‘S’ is given by
- JEE Main - 2023
- Physics
- Electric Flux
- The electric charges are distributed in a small volume. The flux of the electric field through a sphere of radius 10 cm surrounding the total charge is 20 Vm. The flux over a concentric sphere of radius 20 cm will be:
- CUET (UG) - 2023
- Physics
- Electric Flux
Questions Asked in JEE Advanced exam
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
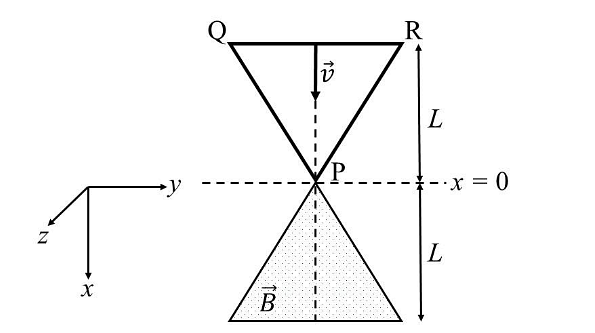
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0? - Two beads, each with charge q and mass m, are on a horizontal, frictionless, non-conducting, circular hoop of radius R. One of the beads is glued to the hoop at some point, while the other one performs small oscillations about its equilibrium position along the hoop. The square of the angular frequency of the small oscillations is given by [ \(\epsilon_0 \)is the permittivity of free space.]
- JEE Advanced - 2024
- Moving charges and magnetism
- A group of 9 students, s1, s2,…., s9, is to be divided to form three teams X, Y and Z of sizes 2, 3, and 4, respectively. Suppose that s1 cannot be selected for the team X and s2 cannot be selected for the team Y. Then the number of ways to form such teams, is _______.
- JEE Advanced - 2024
- Combinations
- Let \(\vec{p}=2\hat{i}+\hat{j}+3\hat{k}\) and \(\vec{q}=\hat{i}-\hat{j}+\hat{k}\). If for some real numbers α, β and γ we have
\(15\hat{i}+10\hat{j}+6\hat{k}=α(2\vec{p}+\vec{q})+β(\vec{p}-2\vec{q})+γ(\vec{p}\times\vec{q})\),
then the value of γ is ________.- JEE Advanced - 2024
- Vector Algebra
- Let X be a random variable, and let P(X = x) denote the probability that X takes the value x. Suppose that the points (x, P(X = x)), x = 0,1,2,3,4, lie on a fixed straight line in the xy -plane, and P(X = x) = 0 for all x ∈ R - {0,1,2,3,4}. If the mean of X is \(\frac{5}{2}\) , and the variance of X is α, then the value of 24α is ______.
- JEE Advanced - 2024
- Probability
Concepts Used:
Electric Flux
Electric flux is a measure of the strength of an electric field passing through a surface. It is defined as the electric field strength times the surface area perpendicular to the electric field. Electric flux is a scalar quantity and is denoted by the symbol ΦE.
The electric flux through a closed surface is equal to the net charge enclosed by that surface, divided by the electric constant. This relationship is known as Gauss's law and is one of the four Maxwell's equations that describe the behavior of electric and magnetic fields.
Electric flux is an important concept in electromagnetism and is used to describe the behavior of electric fields and charges. It is also used to calculate the electric field strength, which is the rate of change of electric flux with respect to distance.
The unit of electric flux is the volt-meter (V m), which is equivalent to the unit of electric field strength. Electric flux has many practical applications, such as in the design and operation of capacitors, electric motors, and generators. It is also used in electrostatic precipitators, which are devices used to remove particulate matter from industrial emissions.
Understanding electric flux is crucial for the development and advancement of modern technology, as it is a fundamental concept in electromagnetism and plays a crucial role in many practical applications.



