A circle of diameter 8 inches is inscribed in a triangle ABC where ∠ABC = 90°. If BC = 10 inches then the area of the triangle in square inches is
Correct Answer: 120
Solution and Explanation
Given that triangle ABC is a right triangle with ∠ABC = 90° and BC = 10 inches, and there's an inscribed circle with diameter 8 inches.
The radius of the circle, \( r \), is \( \frac{8}{2} = 4 \) inches.
Now, for a right triangle with an inscribed circle, the radius of the inscribed circle can be represented in terms of the triangle's legs (the two shorter sides) as follows:
\( r \) = \( \frac{a + b - c}{2} \)
Where:
- \( a \) and \( b \) are the lengths of the two legs of the triangle
- \( c \) is the hypotenuse (BC in this case, which is 10 inches)
Given that \( r = 4 \) inches and \( c = 10 \) inches, we can set up the following equation:
\( 4 \) = \( \frac{a + b - 10}{2} \)
From which:
\( a + b = 18 \) ... equation (1)
Now, we know that the sum of the lengths of the two legs of the right triangle is equal to the diameter of the inscribed circle. Therefore, \( a + b = 8 \) inches. But this conflicts with equation (1), so let's reconsider.
The tangent drawn from a point to a circle is perpendicular to the radius through the point of contact. Given the circle is inscribed inside the triangle, the two legs of the triangle can be considered tangents to the circle.
Thus, the length from the right angle to the circle along leg \( a \) would be \( r \), and the length from the right angle to the circle along leg \( b \) would also be \( r \). This would divide each of the legs of the triangle into two parts.
Let \( a \) be the side that's adjacent to side \( c \) and \( b \) be the side that's opposite side \( c \). Then, \( a \) can be split into two lengths: 4 inches and \( a - 4 \) inches. Similarly, \( b \) can be split into 4 inches and \( b - 4 \) inches.
Using the Pythagorean theorem:
\( a^2 + b^2 = c^2 \)
Substituting the known value of \( c \) (10 inches): \( a^2 + b^2 = 100 \) ... equation (2)
Also, given the geometry of the inscribed circle and the right triangle, the two smaller triangles formed are also similar to triangle ABC. Using their properties and the relationships of the sides:
\( a = 2r + b - 4 \) and \( b = 2r + a - 4 \)
Substituting the value of \( r \) (4 inches) in the above equations: \( a = b + 4 \) ... equation (3)
Using equations (2) and (3):
\( (b + 4)^2 + b^2 = 100 \)
Expanding and simplifying:
\( 2b^2 + 8b - 84 = 0 \)
Solving this quadratic equation for \( b \) gives:
\( b = 6 \) or \( b = -7 \)
The negative value doesn't make sense in this context, so we discard it.
If \( b = 6 \), then \( a = b + 4 = 10 \).
Now, the area of triangle ABC is:
\( \frac{1}{2} \times a \times b = \frac{1}{2} \times 10 \times 6 = 30 square inches.
Top Questions on Geometry
- A farmer has a triangular plot of land. One side of the plot, henceforth called the base, is 300 feet long and the other two sides are equal. The perpendicular distance, from the corner of the plot, where the two equal sides meet, to the base, is 200 feet.
To counter the adverse effect of climate change, the farmer wants to dig a circular pond. He plans that half of the circular area will be inside the triangular plot and the other half will be outside, which he will purchase at the market rate from his neighbour. The diameter of the circular plot is entirely contained in the base and the circumference of the pond touches the two equal sides of the triangle from inside.
If the market rate per square feet of land is Rs. 1400, how much does the farmer must pay to buy the land from his neighbour for the pond? (Choose the closest option.) - Consider a right-angled triangle ABC, right angled at B. Two circles, each of radius r, are drawn inside the triangle in such a way that one of them touches AB and BC, while the other one touches AC and BC. The two circles also touch each other (see the image below).
If AB = 18 cm and BC = 24 cm, then find the value of r.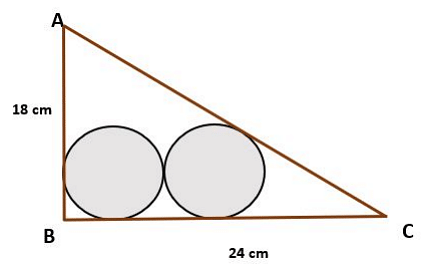
- A group of boys is practising football in a rectangular ground. Raju and Ratan are standing at the two opposite mid-points of the two shorter sides. Raju has the ball, who passes it to Rivu, who is standing somewhere on one of the longer sides. Rivu holds the ball for 3 seconds and passes it to Ratan. Ratan holds the ball for 2 seconds and passes it back to Raju. The path of the ball from Raju to Rivu makes a right angle with the path of the ball from Rivu to Ratan. The speed of the ball, whenever passed, is always 10 metre per second, and the ball always moves on straight lines along the ground.
Consider the following two additional pieces of information:
I. The dimension of the ground is 80 metres × 50 metres.
II. The area of the triangle formed by Raju, Rivu and Ratan is 1000 square metres.
Consider the problem of computing the following: how many seconds does it take for Raju to get the ball back since he passed it to Rivu? Choose the correct option. - Given below are two statements
Statement I =If two chords XY and ZT of a circle intersects internally at point P,then PX-PYPZ-PT
Statement II =If two chords XY and ZT of a circle intersect internally at point P,then PXZ and PTY are similar triangles
In the light of the above statements, choose the correct answer from the options given below - In the given figure the value of angle ‘x’ is _________
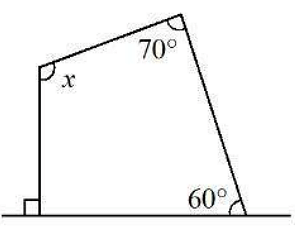
Questions Asked in CAT exam
- If \(\sqrt{5x+9}\)+\(\sqrt{5x-9}\)=\(3(2-\sqrt2)\) then \(\sqrt{10x+9}\) is equal to
- CAT - 2023
- Square and Square Roots
- Suppose \(f(x,y)\) is a real-valued function such that \(f(3x+2y,2x-5y)=19x\), for all real numbers \(x\) and \(y\) . The value of x for which \(f(x,2x) = 27\) , is
- CAT - 2023
- Functions
- If \(x\) is a positive real number such that \(x^8+\bigg(\frac{1}{x}\bigg)^8=47\) , then the value of \(x^9+\bigg(\frac{1}{x}\bigg)^9\) is
- CAT - 2023
- Basics of Numbers
- The sum of the first two natural numbers, each having 15 factors (including 1 and the number itself), is
- CAT - 2023
- Number Systems
- The value of \(1+\bigg(1+\frac{1}{3}\bigg)\frac{1}{4}+\bigg(1+\frac{1}{3}+\frac{1}{9}\bigg)\frac{1}{16}+\bigg(1+\frac{1}{3}+\frac{1}{9}+\frac{1}{27}\bigg)\frac{1}{64}+....\),is
- CAT - 2023
- Quick Math
CAT Notification
 CAT 2024 Registration Extended till Sept 20, Apply Now!Sep 13, 2024
CAT 2024 Registration Extended till Sept 20, Apply Now!Sep 13, 2024


