The ratio of specific heats
\((\frac{c_p}{c_v}) \)
in terms of degree of freedom (f) is given by:
The ratio of specific heats
\((\frac{c_p}{c_v}) \)
in terms of degree of freedom (f) is given by:
- \((1+\frac{f}{3})\)
- \((1+\frac{2}{f})\)
- \((1+\frac{f}{2})\)
- \((1+\frac{1}{f})\)
The Correct Option is A
Solution and Explanation
The correct option is(B): \((1+\frac{1}{f})\).
\(\frac{c_p}{c_v}=γ\)
\(c_v=(\frac{f}{2})R\)
and
\(C_p-C_v=R\)
\(⇒\frac{c_p}{c}=\frac{1+\frac{f}{2}}{\frac{f}{2}}\)
\(1+\frac{2}{f}\)
Top Questions on Heat Transfer
- In given circuit, reading of voltmeter is 1 V, then resistance of
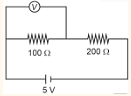
- JEE Main - 2024
- Physics
- Heat Transfer
- A solid slab of thickness \( H1 \) is initially at a uniform temperature \( T0 \). At time \( t = 0 \), the temperature of the top surface at \( y = H1 \) is increased to \( T1 \), while the bottom surface at \( y = 0 \) is maintained at \( T0 \) for \( t \geq 0 \). Assume heat transfer occurs only in the \( y \)-direction, and all thermal properties of the slab are constant. The time required for the temperature at \( y = \frac{H1}{2} \) to reach 99% of its final steady value is \( T1 \). If the thickness of the slab is doubled to \( H2 = 2H1 \), and the time required for the temperature at \( y = \frac{H2}{2} \) to reach 99% of its final steady value is \( T2 \), then \( \frac{T2}{T1} \) is .
- GATE CH - 2024
- Heat Transfer
- Heat Transfer
- Ice at temperature –10°C is converted to steam at 100°C, the curve plotted between temperature (T) and time (t) when it is being heated by constant power source is
- JEE Main - 2024
- Physics
- Heat Transfer
- The temperatures of two large parallel plates of equal emissivity are 900 K and 300 K. A reflection radiation shield of low emissivity and negligible conductive resistance is placed parallelly between them. The steady-state temperature of the shield, in K, is
- GATE CH - 2024
- Heat Transfer
- Heat Transfer
- The opposite faces of a metal slab of thickness 5 cm and thermal conductivity 400 W m\(^{-1}\) °C\(^{-1}\) are maintained at 500 °C and 200 °C. The area of each face is 0.02 m\(^2\). Assume that the heat transfer is steady and occurs only in the direction perpendicular to the faces. The magnitude of the heat transfer rate, in kW, rounded off to the nearest integer, is ____.
- GATE CH - 2024
- Heat Transfer
- Heat Transfer
Questions Asked in JEE Main exam
- Let \[\vec{a} = \hat{i} + \hat{j} + \hat{k}, \quad \vec{b} = -\hat{i} - 8\hat{j} + 2\hat{k}, \quad \text{and} \quad \vec{c} = 4\hat{i} + c_2\hat{j} + c_3\hat{k} \]be three vectors such that \[\vec{b} \times \vec{a} = \vec{c} \times \vec{a}.\]If the angle between the vector $\vec{c}$ and the vector $3\hat{i} + 4\hat{j} + \hat{k}$ is $\theta$, then the greatest integer less than or equal to $\tan^2 \theta$ is:
- JEE Main - 2024
- Vector Algebra
- 10 mL of gaseous hydrocarbon on combustion gives 40 mL of CO\(_2\)(g) and 50 mL of water vapour. The total number of carbon and hydrogen atoms in the hydrocarbon is ______ .
- JEE Main - 2024
- Hydrocarbons
- If each term of a geometric progression \( a_1, a_2, a_3, \dots \) with \( a_1 = \frac{1}{8} \) and \( a_2 \neq a_1 \), is the arithmetic mean of the next two terms and \( S_n = a_1 + a_2 + \dots + a_n \), then \( S_{20} - S_{18} \) is equal to
- JEE Main - 2024
- Arithmetic Mean
A body of mass 1000 kg is moving horizontally with a velocity of 6 m/s. If 200 kg extra mass is added, the final velocity (in m/s) is:
- JEE Main - 2024
- speed and velocity
- $\textbf{Choose the correct statements about the hydrides of group 15 elements.}$
A. The stability of the hydrides decreases in the order \(\text{NH}_3 > \text{PH}_3 > \text{AsH}_3 > \text{SbH}_3 > \text{BiH}_3\)
B. The reducing ability of the hydrides increases in the order \(\text{NH}_3 < \text{PH}_3 < \text{AsH}_3 < \text{SbH}_3 < \text{BiH}_3\)
C. Among the hydrides, \(\text{NH}_3\) is a strong reducing agent while \(\text{BiH}_3\) is a mild reducing agent.
D. The basicity of the hydrides increases in the order \(\text{NH}_3 < \text{PH}_3 < \text{AsH}_3 < \text{SbH}_3 < \text{BiH}_3\)
Choose the most appropriate from the option given below:- JEE Main - 2024
- p -Block Elements
Concepts Used:
Temperature Dependence of Resistance
The temperature dependence of resistance is a fundamental property of all materials that conduct electricity. Generally, the resistance of a conductor increases with an increase in temperature. This phenomenon is known as a positive temperature coefficient of resistance.
The reason for this temperature dependence of resistance is related to the interaction of electrons with the crystal lattice of the material. At lower temperatures, the lattice vibrations are minimal, and the electrons are free to move through the material with minimal scattering. This results in a low resistance to the flow of current. However, as the temperature increases, the lattice vibrations increase, causing the electrons to scatter more frequently, which increases resistance.
This phenomenon is governed by the relationship between resistance and temperature known as the temperature coefficient of resistance. The temperature coefficient of resistance is defined as the rate at which resistance changes with respect to temperature. The temperature coefficient of resistance is positive for most metals and semiconductors, meaning that resistance increases with increasing temperature.
However, there are a few materials, such as carbon and certain semiconductors, which exhibit a negative temperature coefficient of resistance. In these materials, the resistance decreases as the temperature increases.
The temperature dependence of resistance has important practical implications in the design and operation of electrical circuits and devices. For example, it is essential to consider the effect of temperature on the resistance of electronic components to ensure reliable and efficient operation of devices over a range of temperatures.



