Mass spectrometric analysis of potassium and argon atoms in a Moon rock sample shows that the ratio of the number of (stable) ${ }^{40} Ar$ atoms present to the number of (radioactive) ${ }^{40} K$ atoms is $10.3$. Assume that all the argon atoms were produced by the decay of potassium atoms, with a half-life of $1.25 \times 10^{9} yr$. How old is the rock?
- $2.95 \times 10^{11}\,yr$
- $2.95 \times 10^{9}\,yr$
- $4.37 \times 10^{9}\,yr$
- $4.37 \times 10^{11}\,yr$
The Correct Option is C
Solution and Explanation
Top Questions on Electromagnetic Spectrum
- Arrange the following in the ascending order of wavelength:
(A) Gamma rays (\( \lambda_1 \))
(B) X-ray (\( \lambda_2 \))
(C) Infrared waves (\( \lambda_3 \))
(D) Microwaves (\( \lambda_4 \))
Choose the most appropriate answer from the options given below:- JEE Main - 2024
- Physics
- Electromagnetic Spectrum
- Which of the following is/are responsible for the formation of Rainbow?
(A) Dispersion of light
(B) Interference of light
(C) Reflection of light
(D) Refraction of light
Choose the correct answer from the options given below:- CUET (UG) - 2023
- Physics
- Electromagnetic Spectrum
- Following are the wavelength of some constituents of the electromagnetic spectrum. The wavelength range that are used in Radar system for Aircraft navigation is:
(A) 1 mm to 700 nm
(B) 0.1 m to 1 mm
(C) 400 nm to 1 nm
(D) < 10-3 nm
(E) > 1m
Choose the correct answer from the options given below:- CUET (UG) - 2023
- Physics
- Electromagnetic Spectrum
- A thin conducting rod MN of mass 20 gm, length 25 cm, and resistance 10Ω is held on frictionless long perfectly conducting vertical rails as in the figure. There is the uniform magnetic field B0=4T directed perpendicular to the plane of the rod-rail arrangement. the rod is released from rest at time t=0 and it moves down along the rails assuming air drag is negligible. Match each quantity in L-I with an appropriate value from L-II and choose the correct options(g=10ms\(^{-2}\) and e\(^{-1}\)=0.4)
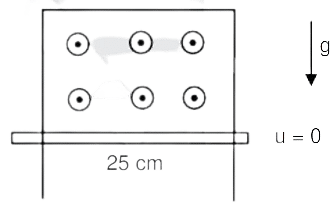
List-I
List-II (P) At t=0.2s, the magnitude of induced emf in volt (1) 0.08 (Q) At t=0.2s, the magnitude of magnetic force in N (2) 0.14 (R) At t=0.2s, the power dissipated at heat in watt (3) 1.20 (S) The magnitude terminal velocity of the rod in ms\(^{-1}\) (4) 0.12 (5) 2.00 - JEE Advanced - 2023
- Physics
- Electromagnetic Spectrum
- The oscillating magnetic field in a plane electromagnetic wave is given by By = \(5 × 10^{–6}\) \(sin\;1000\;π(5x – 4 × 108\;t)T\). The amplitude of electric field will be:
- JEE Main - 2022
- Physics
- Electromagnetic Spectrum
Questions Asked in AIIMS exam
Given below are two statements, one is labelled as Assertion A and the other is labelled as Reason R
Assertion (A) : 02 is liberated in the non-cyclic photophosphorylation.
Reason (R) : Liberation of oxygen is due to photolysis of water.
In the light of the above statements, choose the correct answer from the options given below
- AIIMS - 2019
- Photosynthesis in higher plants
- Match the following column I with column II.
- AIIMS - 2019
- cloning
Given below are two statements, one is labelled as Assertion A and the other is labelled as Reason R
Assertion (A) : The Cro-Magnon man was the direct ancestor of the living modern man.
Reason (R) : Cro-Magnon man had slightly prognathous face.
In the light of the above statements, choose the correct answer from the options given below
- AIIMS - 2019
- evolution
- Given below are two statements, one is labelled as Assertion A and the other is labelled as Reason R
Assertion: Orbit of a satellite is within the gravitational field of earth whereas escaping is beyond the gravitational field of earth.
Reason: Orbital velocity of a satellite is greater than its escape velocity.
In the light of the above statements, choose the correct answer from the options given below- AIIMS - 2019
- Gravitation
Given below are two statements, one is labelled as Assertion A and the other is labelled as Reason R
Assertion (A) : In eukaryotes, transcription occurs in nucleus.
Reason (R) : In bacteria, transcription and translation occurs in cytoplasm.
In the light of the above statements, choose the correct answer from the options given below
- AIIMS - 2019
- Transcription
Concepts Used:
Electromagnetic Spectrum
The term used by scientists to describe the entire range of light that exists is the electrostatic spectrum. Light is a wave of alternating electric and magnetic fields. The propagation of light doesn't vary from waves crossing an ocean. Like any other wave, light also has a few fundamental properties that describe it. One is its frequency. The frequency is measured in Hz, which counts the number of waves that pass by a point in one second.
The electromagnetic waves that your eyes detect are visible light and oscillate between 400 and 790 terahertz (THz). That’s several hundred trillion times a second.



