Let $f:(0, \infty) \rightarrow R$ be given by $f(x)=\int\limits_{1 / x}^{x} e^{-\left(t+\frac{1}{t}\right)} \frac{d t}{t}$, then
- $f(x)$ is monotonically increasing on $[1, \infty$ )
- $f(x)$ is monotonically decreasing on $(0,1)$
- $f(x)+f\left(\frac{1}{x}\right)=0$, for all $x \in(0, \infty)$
- $f\left(2^{x}\right)$ is an odd function of $x$ on $R$.
The Correct Option is D
Solution and Explanation
Given that
\(f\left(x\right)=\int\limits_{1/x}^{x} e^{-(t+\frac{1}{t})} d t\)
⇒\( \frac{d}{dx}f(x) = \frac{e^{-x+\frac{1}{x}}}{x}\frac{dx}{dx}-\frac{e^{-(\frac1 x+x)}}{1/x}x \frac{d \frac{1}{x}}{dx}\)
= \(\frac{e^{-(x+\frac{1}{x})}}{x} + xe^{-(x+\frac{1}{x})}x\frac{-1}{x^2}\)
= \(e^{-(x+\frac{1}{x})} + \frac{1}{x}e^{-(x+\frac{1}{x})}\)
= \(2e^{-(x+\frac{1}{x})}= 0\)
Hence, \(f(x)+\)\(f(\frac{1}{x}) = \)
\[\int\limits_{1/x}^{x} \frac{e^{-(t+\frac{1}{t}})} {t}dt+\int\limits_{x}^{1/x} \frac{e^{-(t+\frac{1}{t}})}{t} d t\]\[\int\limits_{1/x}^{1/x} \frac{e^{-(t+\frac{1}{t})}}{t} d t=0\]Now,
\(f(2^x)+f(\frac{1}{2^x})=f(2^x)+f(2^x)=0\)
Therefore, \(f(2^x) \) is an odd function.
Note, Let 2x= μ
log2μ =x
∴ f(2x) = h(x) an odd function
Then h(-x)
Top Questions on Derivatives of Functions in Parametric Forms
- If \( 2 \tan^2 \theta - 5 \sec \theta = 1 \) has exactly 7 solutions in the interval \(\left[ 0, \frac{n\pi}{2} \right],\) for the least value of \( n \in \mathbb{N} \) then \(\sum_{k=1}^{n} \frac{k}{2^k}\) is equal to:
- JEE Main - 2024
- Mathematics
- Derivatives of Functions in Parametric Forms
- Let $x=\sin \left(2 \tan ^{-1} \alpha\right)$ and $y=\sin \left(\frac{1}{2} \tan ^{-1} \frac{4}{3}\right)$ If $S =\left\{\alpha \in R : y ^2=1- x \right\}$, then $\displaystyle\sum_{\alpha \in S } 16 \alpha^3$ is equal to ______
- JEE Main - 2023
- Mathematics
- Derivatives of Functions in Parametric Forms
- If x = 3 tan t and y = 3 sec t, then find \(\frac{d^2y}{dx^2} \, at\,t=\frac{\pi}{4}\), is:
- MHT CET - 2023
- Mathematics
- Derivatives of Functions in Parametric Forms
- The equation \(r^2=cos^2(\theta-\frac{\pi}{3})=2\) represents
- WBJEE - 2023
- Mathematics
- Derivatives of Functions in Parametric Forms
- Which of the following statements are true?
- WBJEE - 2023
- Mathematics
- Derivatives of Functions in Parametric Forms
Questions Asked in JEE Advanced exam
- A closed vessel contains 10 g of an ideal gas X at 300 K, which exerts 2 atm pressure. At the same temperature, 80 g of another ideal gas Y is added to it and the pressure becomes 6 atm. The ratio of root mean square velocities of X and Y at 300 K is
- JEE Advanced - 2024
- States of matter
- Let the function \(f:[1,\infin)→\R\) be defined by
\(f(t) = \begin{cases} (-1)^{n+1}2, & \text{if } t=2n-1,n\in\N, \\ \frac{(2n+1-t)}{2}f(2n-1)+\frac{(t-(2n-1))}{2}f(2n+1) & \text{if } 2n-1<t<2n+1,n\in\N. \end{cases}\)
Define \(g(x)=\int\limits_{1}^{x}f(t)dt,x\in(1,\infin).\) Let α denote the number of solutions of the equation g(x) = 0 in the interval (1, 8] and \(β=\lim\limits_{x→1+}\frac{g(x)}{x-1}\). Then the value of α + β is equal to _____.- JEE Advanced - 2024
- Integral Calculus
- A dimensionless quantity is constructed in terms of electronic charge \(e\), permittivity of free space \(\epsilon_0\) , Planck’s constant ℎ, and speed of light c. If the dimensionless quantity is written as \(e^\alpha\epsilon_0^\beta h^\gamma c^\delta\)and n is a non-zero integer, then\((\alpha, \beta,\gamma,\delta)\) is given by
- JEE Advanced - 2024
- Semiconductor electronics: materials, devices and simple circuits
- A block of mass \(5 kg\) moves along the \(x-\)direction subject to the force \(F = (−20x + 10) N,\) with the value of \(x \) in metre. At time \(t = 0 s,\) it is at rest at position \(x = 1 m\). The position and momentum of the block at \(t = (\pi/4)\) s are
- JEE Advanced - 2024
- Work-energy theorem
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
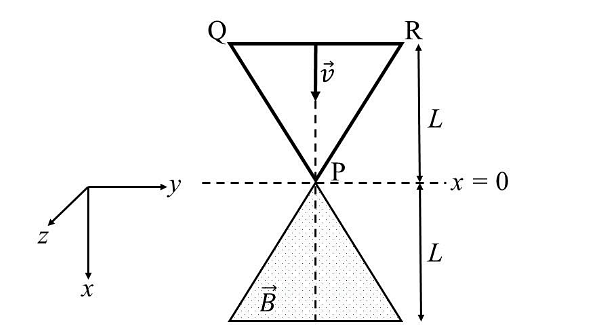
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0?
Concepts Used:
Methods of Integration
Given below is the list of the different methods of integration that are useful in simplifying integration problems:
Integration by Parts:
If f(x) and g(x) are two functions and their product is to be integrated, then the formula to integrate f(x).g(x) using by parts method is:
∫f(x).g(x) dx = f(x) ∫g(x) dx − ∫(f′(x) [ ∫g(x) dx)]dx + C
Here f(x) is the first function and g(x) is the second function.
Method of Integration Using Partial Fractions:
The formula to integrate rational functions of the form f(x)/g(x) is:
∫[f(x)/g(x)]dx = ∫[p(x)/q(x)]dx + ∫[r(x)/s(x)]dx
where
f(x)/g(x) = p(x)/q(x) + r(x)/s(x) and
g(x) = q(x).s(x)
Integration by Substitution Method
Hence the formula for integration using the substitution method becomes:
∫g(f(x)) dx = ∫g(u)/h(u) du
Integration by Decomposition
Reverse Chain Rule
This method of integration is used when the integration is of the form ∫g'(f(x)) f'(x) dx. In this case, the integral is given by,
∫g'(f(x)) f'(x) dx = g(f(x)) + C



