Question:
An ideal gas of density $\rho=02 \,kg \, m ^{-3}$ enters a chimney of height $h$ at the rate of $\alpha=08 \,kg \,s ^{-1}$ from its lower end, and escapes through the upper end as shown in the figure The cross-sectional area of the lower end is $A_1=01 \, m ^2$ and the upper end is $A_2=04 \, m ^2$ The pressure and the temperature of the gas at the lower end are $600 \,Pa$ and $300 \,K$, respectively, while its temperature at the upper end is $150 \,K$ The chimney is heat insulated so that the gas undergoes adiabatic expansion Take $g=10 \,ms ^{-2}$ and the ratio of specific heats of the gas $\gamma=2$ Ignore atmospheric pressure Which of the following statement(s) is(are) correct?

An ideal gas of density $\rho=02 \,kg \, m ^{-3}$ enters a chimney of height $h$ at the rate of $\alpha=08 \,kg \,s ^{-1}$ from its lower end, and escapes through the upper end as shown in the figure The cross-sectional area of the lower end is $A_1=01 \, m ^2$ and the upper end is $A_2=04 \, m ^2$ The pressure and the temperature of the gas at the lower end are $600 \,Pa$ and $300 \,K$, respectively, while its temperature at the upper end is $150 \,K$ The chimney is heat insulated so that the gas undergoes adiabatic expansion Take $g=10 \,ms ^{-2}$ and the ratio of specific heats of the gas $\gamma=2$ Ignore atmospheric pressure Which of the following statement(s) is(are) correct?


Updated On: Jul 14, 2024
- The pressure of the gas at the upper end of the chimney is $300\, Pa$.
- The velocity of the gas at the lower end of the chimney is $40 \,ms ^{-1}$ and at the upper end is $20\, ms ^{-1}$.
- The height of the chimney is $590 \,m$.
- The density of the gas at the upper end is $0.05\, kg\, m ^{-3}$.
Hide Solution
Verified By Collegedunia
The Correct Option is B
Solution and Explanation

\(\frac{dm}{dt} = p_1 A_1 v_1 = 0.8 \, \text{kg/s} \, A\)
\(v_1 = \frac{0.8}{0.2 \times 0.1} = 40 \, \text{m/s}\)
g = 10 m/s2
\(\gamma = 2\)
Gas undergoes adiabatic expansion,
\(p_1 - \gamma T^{\gamma} = \text{Constant}\)
\(\frac{P_2}{P_1}=(\frac{T_1}{T_2})^{\frac{r}{1-\gamma}}\)
\(P_2=\frac{600}{4}=150P_a\)
Now \(\rho∝\frac{P}{T}\)
\(\frac{\rho_1}{\rho_2}=(\frac{P_1}{P_2})(\frac{T_1}{T_2})\)
\((\frac{150}{600})(\frac{300}{150})=\frac{1}{2}\)
Now
\(P_1 A_1 \Delta x_1 - P_2 A_2 \Delta x_2 = 2 mV_1 - mV_2 + mgh_2 - mgh_1 + \frac{f}{2}(P_2 V_2 - P_1 V_1)\)
Simplifying we get. \(\frac{V_2}{V_1} - \frac{V_1}{V_2} = \frac{2P}{gh} \frac{m}{m}\)
\(⇒\frac{2\times600}{0.2}-\frac{2\times150}{0.1}\)
\(=\frac{20^2-40^2}{2}+10h\)
\(h = 360 m\)
Was this answer helpful?
0
4
Top Questions on Kinetic molecular theory of gases
- Find the ratio of the root mean square speed of oxygen gas molecules to that of hydrogen gas molecules, if the temperature of both gases is the same.
- JEE Main - 2023
- Physics
- Kinetic molecular theory of gases
- At \(300 K\) the rms speed of oxygen molecules is \(\sqrt {\frac {\alpha+5}{\alpha}}\) times to that of its average speed in the gas. Then, the value of \(\alpha\) will be
(used \(\pi=\frac {22}{7}\))- JEE Main - 2023
- Physics
- Kinetic molecular theory of gases
- The number of air molecules per cm3 increased from 3 × 1019 to 12 × 1019. The ratio of collision frequency of air molecules before and after the increase in the number respectively is :
- JEE Main - 2023
- Physics
- Kinetic molecular theory of gases
- The root mean square speed of molecules of nitrogen gas at 27°C is approximately : (Given mass of a nitrogen molecule = \(4.6 × 10^{–26}\) kg and take Boltzmann constant KB = \(1.4 × 10^{–23}\) JK–1 )
- JEE Main - 2023
- Physics
- Kinetic molecular theory of gases
- The mean free path of molecules of a certain gas at STP is 1500d, where d is the diameter of the gas molecules. While maintaining the standard pressure, the mean free path of the molecules at 373K is approximately
- JEE Main - 2023
- Physics
- Kinetic molecular theory of gases
View More Questions
Questions Asked in JEE Advanced exam
- A closed vessel contains 10 g of an ideal gas X at 300 K, which exerts 2 atm pressure. At the same temperature, 80 g of another ideal gas Y is added to it and the pressure becomes 6 atm. The ratio of root mean square velocities of X and Y at 300 K is
- JEE Advanced - 2024
- States of matter
- Let the function \(f:[1,\infin)→\R\) be defined by
\(f(t) = \begin{cases} (-1)^{n+1}2, & \text{if } t=2n-1,n\in\N, \\ \frac{(2n+1-t)}{2}f(2n-1)+\frac{(t-(2n-1))}{2}f(2n+1) & \text{if } 2n-1<t<2n+1,n\in\N. \end{cases}\)
Define \(g(x)=\int\limits_{1}^{x}f(t)dt,x\in(1,\infin).\) Let α denote the number of solutions of the equation g(x) = 0 in the interval (1, 8] and \(β=\lim\limits_{x→1+}\frac{g(x)}{x-1}\). Then the value of α + β is equal to _____.- JEE Advanced - 2024
- Integral Calculus
- A dimensionless quantity is constructed in terms of electronic charge \(e\), permittivity of free space \(\epsilon_0\) , Planck’s constant ℎ, and speed of light c. If the dimensionless quantity is written as \(e^\alpha\epsilon_0^\beta h^\gamma c^\delta\)and n is a non-zero integer, then\((\alpha, \beta,\gamma,\delta)\) is given by
- JEE Advanced - 2024
- Semiconductor electronics: materials, devices and simple circuits
- A block of mass \(5 kg\) moves along the \(x-\)direction subject to the force \(F = (−20x + 10) N,\) with the value of \(x \) in metre. At time \(t = 0 s,\) it is at rest at position \(x = 1 m\). The position and momentum of the block at \(t = (\pi/4)\) s are
- JEE Advanced - 2024
- Work-energy theorem
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
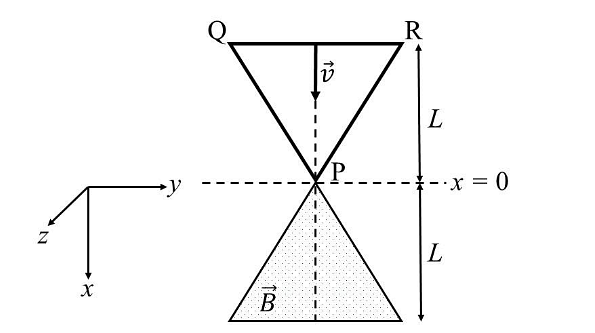
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0?
View More Questions
Concepts Used:
Kinetic Molecular Theory of Gases
Postulates of Kinetic Theory of Gases:
- Gases consist of particles in constant, random motion. They continue in a straight line until they collide with each other or the walls of their container.
- Particles are point masses with no volume. The particles are so small compared to the space between them, that we do not consider their size in ideal gases.
- Gas pressure is due to the molecules colliding with the walls of the container. All of these collisions are perfectly elastic, meaning that there is no change in energy of either the particles or the wall upon collision. No energy is lost or gained from collisions. The time it takes to collide is negligible compared with the time between collisions.
- The kinetic energy of a gas is a measure of its Kelvin temperature. Individual gas molecules have different speeds, but the temperature and
kinetic energy of the gas refer to the average of these speeds. - The average kinetic energy of a gas particle is directly proportional to the temperature. An increase in temperature increases the speed in which the gas molecules move.
- All gases at a given temperature have the same average kinetic energy.
- Lighter gas molecules move faster than heavier molecules.




