Question:
An electron in the Coulomb field of a proton is in the following state of coherent superposition of orthonormal states \( \psi_{n i m} \):\[ \psi = \frac{1}{3} \psi_{100} + \frac{1}{\sqrt{3}} \psi_{210} + \frac{\sqrt{5}}{3} \psi_{320} \]Let \( E_1, E_2, \) and \( E_3 \) represent the first three energy levels of the system. A sequence of measurements is done on the same system at different times. Energy is measured first at time \( t_1 \) and the outcome is \( E_2 \). Then total angular momentum is measured at time \( t_2 > t_1 \), and finally, energy is measured again at \( t_3 > t_2 \). The probability of finding the system in a state with energy \( E_2 \) after the final measurement is \( \frac{P}{9} \). The value of \( P \) is ______ (in integer).
An electron in the Coulomb field of a proton is in the following state of coherent superposition of orthonormal states \( \psi_{n i m} \):\[ \psi = \frac{1}{3} \psi_{100} + \frac{1}{\sqrt{3}} \psi_{210} + \frac{\sqrt{5}}{3} \psi_{320} \]Let \( E_1, E_2, \) and \( E_3 \) represent the first three energy levels of the system. A sequence of measurements is done on the same system at different times. Energy is measured first at time \( t_1 \) and the outcome is \( E_2 \). Then total angular momentum is measured at time \( t_2 > t_1 \), and finally, energy is measured again at \( t_3 > t_2 \). The probability of finding the system in a state with energy \( E_2 \) after the final measurement is \( \frac{P}{9} \). The value of \( P \) is ______ (in integer).
Updated On: Jul 12, 2024
Hide Solution
Verified By Collegedunia
Correct Answer: 9
Solution and Explanation
The correct Answer is:9 or 9 Approx
Was this answer helpful?
0
0
Top Questions on Electric Charge
- Two point charges of charge \( +q \) each are placed a distance \( 2d \) apart. A grounded solid conducting sphere of radius \( a \) is placed midway between them. Assume \( a^2 \ll d^2 \). Which of the following statements is/are true?
- GATE PH - 2024
- Physics
- Electric Charge
- A particle of mass \( m \) in an infinite potential well of width \( a \) is subjected to a perturbation \( V' = \frac{h^2}{40ma^2} \) as shown in the figure, where \( h \) is Planck's constant.
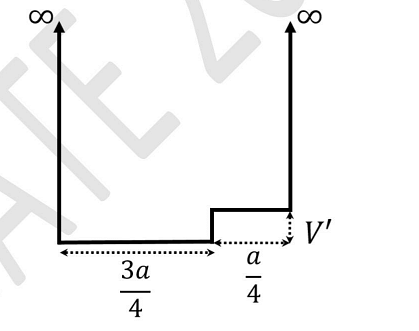
The first-order energy shift of the fourth energy eigenstate due to this perturbation is \( \frac{h^2}{Nma^2} \). The value of \( N \) is ____ (in integer).- GATE PH - 2024
- Physics
- Electric Charge
- The curves \( P \) and \( Q \) schematically show the variation of X-ray intensity with wavelength at two different accelerating voltages for a given target material. In the figure, \( \lambda_1 = 0.25 \) Å, \( \lambda_2 = 0.5 \) Å, \( \lambda_3 = 1.0 \) Å, and \( \lambda_4 = 2.25 \) Å. Take Planck's constant as \( 6.6 \times 10^{-34} \) Js, the speed of light as \( 3 \times 10^8 \) m/s, and the elementary charge as \( 1.6 \times 10^{-19} \) C.

Which of the following statement is/are true?- GATE PH - 2024
- Physics
- Electric Charge
- An electron is moving with the speed of \(1\) \(m/s\) at a distance of \(1\) \(m\), from a large sheet of charge with density \(σ\) \(C/m^2\). Find the maximum value of \(σ\) such that electron hits the sheet after \(1\) \(sec\). (mass of electron = \(9 × 10^{-31}\) kg, Permittivity of free space = \(9\times10^{12}\;C^2/Nm^2\)
- JEE Main - 2024
- Physics
- Electric Charge
- Two charges q and 3q are placed at a distance r from each other. Find the distance from q where the electric field is zero.
- JEE Main - 2024
- Physics
- Electric Charge
View More Questions
Questions Asked in GATE PH exam
- When an unpolarized plane electromagnetic wave in a dielectric medium with refractive index \( n_1 \) is incident on a plane interface separating it from another dielectric medium with refractive index \( n_2 \) (where \( n_2 > n_1 \)), and the angle of incidence is \(\tan^{-1} \left( \frac{n_2}{n_1} \right) \), the following statement is true:
- GATE PH - 2024
- Electromagnetic Waves
- Binding energy and rest mass energy of a two-nucleon bound state are denoted by \( B \) and \( mc^2 \), respectively, where \( c \) is the speed of light. The minimum energy of a photon required to dissociate the bound state is _______.
- If a thermodynamical system is adiabatically isolated and experiences a change in volume under an externally applied constant pressure, then the thermodynamical potential minimized at equilibrium is the
- GATE PH - 2024
- Thermodynamics
- The mean distance between the two atoms of an HD molecule is \( r \), where H and D denote hydrogen and deuterium, respectively. The mass of the hydrogen atom is \( m_H \). The energy difference between the two lowest lying rotational states of HD in multiples of \(\frac{h^2}{m_H r^2}\) is:
- GATE PH - 2024
- atom structure models
- Let \( p(\bar{p}, \bar{q}, t) \) be the phase space density of an ensemble of a system. The Hamiltonian of the system is \( H(p, q) \). If \( \{A, B\} \) denotes the Poisson bracket of \( A \) and \( B \), then \( \frac{dp}{dt} = 0 \) implies
- GATE PH - 2024
- Phase rule
View More Questions



