Question:
A convex lens made of glass has focal length $0.15\, m$ in air. If the refractive index of glass is $3/2$, and that of water is $4/3$ the focal length of lens when immersed in water is
A convex lens made of glass has focal length $0.15\, m$ in air. If the refractive index of glass is $3/2$, and that of water is $4/3$ the focal length of lens when immersed in water is
Updated On: Apr 23, 2024
- 0.15 m
- 0.30 m
- 0.6 m
- 0.45 m
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
Given, $f_{a}=0.15 \,m , \mu_{g}=\frac{3}{2}, \mu_{w}=\frac{4}{3}$
According to Lens maker's formula
$\frac{1}{f} =(\mu-1)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right) \,\,\,\,\,\,$ where $\mu=\frac{\mu_{L}}{\mu_{M}} $
$\frac{1}{f_{a}} =\left(\frac{\mu_{g}}{\mu_{a}}-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right) $
$=\left(\frac{(3 / 2)}{1}-1\right) C\,\,\,\,\,\,\,\, $ where $ C=\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$
or $\,\,\,\frac{1}{f_{a}}=\frac{C}{2}\,\,\,\,\,\,\,\,...(i)$
Also, $\frac{1}{f_{w}}=\left(\frac{\mu_{g}}{\mu_{w}}-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)=\left(\frac{(3 / 2)}{(4 / 3)}-1\right) C$
or $\,\,\,\,\,\frac{1}{f_{w}}=\frac{C}{8}\,\,\,\,\,\,\,\,...(ii)$
From Eqs. (i) and (ii), we get
$\frac{f_{w}}{f_{a}}=\frac{C}{2} \times \frac{8}{C}=4$
or$\,\,\,\,\,\,f_{w}=4 f_{a}$
$=4 \times 0.15=0.6\, m$
According to Lens maker's formula
$\frac{1}{f} =(\mu-1)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right) \,\,\,\,\,\,$ where $\mu=\frac{\mu_{L}}{\mu_{M}} $
$\frac{1}{f_{a}} =\left(\frac{\mu_{g}}{\mu_{a}}-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right) $
$=\left(\frac{(3 / 2)}{1}-1\right) C\,\,\,\,\,\,\,\, $ where $ C=\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$
or $\,\,\,\frac{1}{f_{a}}=\frac{C}{2}\,\,\,\,\,\,\,\,...(i)$
Also, $\frac{1}{f_{w}}=\left(\frac{\mu_{g}}{\mu_{w}}-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)=\left(\frac{(3 / 2)}{(4 / 3)}-1\right) C$
or $\,\,\,\,\,\frac{1}{f_{w}}=\frac{C}{8}\,\,\,\,\,\,\,\,...(ii)$
From Eqs. (i) and (ii), we get
$\frac{f_{w}}{f_{a}}=\frac{C}{2} \times \frac{8}{C}=4$
or$\,\,\,\,\,\,f_{w}=4 f_{a}$
$=4 \times 0.15=0.6\, m$
Was this answer helpful?
4
0
Top Questions on Spherical Mirrors
- Distance between twice-magnified virtual image of an object placed in front of mirror is 15 cm. Find focal length of spherical mirror in cm.
- JEE Main - 2024
- Physics
- Spherical Mirrors
- Distance between virtual image, which is twice the size of object placed in front of mirror and object is 45 cm. The magnitude of focal length of the mirror is _____cm.
- JEE Main - 2024
- Physics
- Spherical Mirrors
- A convex lens of focal length $20\, cm$ is placed in front of convex mirror with principal axis coinciding each other The distance between the lens and mirror is $10\, cm$ A point object is placed on principal axis at a distance of $60 \, cm$ from the convex lens The image formed by combination coincides the object itself The focal length of the convex mirror is ________ $cm$
- JEE Main - 2023
- Physics
- Spherical Mirrors
- The radius of curvature of a spherical mirror is 16 cm. What is the focal length ?
- TS POLYCET - 2023
- Physics
- Spherical Mirrors
- When the object lies at infinite distance in front of concave mirror then the nature of the image is
- WBJEE JENPAS UG - 2023
- Physical Sciences
- Spherical Mirrors
View More Questions
Questions Asked in KCET exam
- If \(\lim\limits_{x \rightarrow 0} \frac{\sin(2+x)-\sin(2-x)}{x}\)= A cos B, then the values of A and B respectively are
- KCET - 2023
- limits of trigonometric functions
- The Curie temperatures of Cobalt and iron are 1400K and 1000K respectively. At T = 1600K , the ratio of magnetic susceptibility of Cobalt to that of iron is
- KCET - 2023
- Magnetism and matter
- A particle is in uniform circular motion. Related to one complete revolution of the particle, which among the stataments is incorrect ?
- KCET - 2023
- Uniform Circular Motion
- The modulus of the complex number \(\frac{(1+i)^2(1+3i)}{(2-6i)(2-2i)}\) is
- KCET - 2023
- complex numbers
- The energy gap of an LED is 2.4 eV. When the LED is switched ‘ON’, the momentum of the emitted photons is
- KCET - 2023
- Semiconductor electronics: materials, devices and simple circuits
View More Questions
Concepts Used:
Spherical Mirrors
A spherical mirror is a mirror which has been cut out of a spherical surface.
There are two kinds of spherical mirrors:
- Convex Mirror
- Concave Mirror
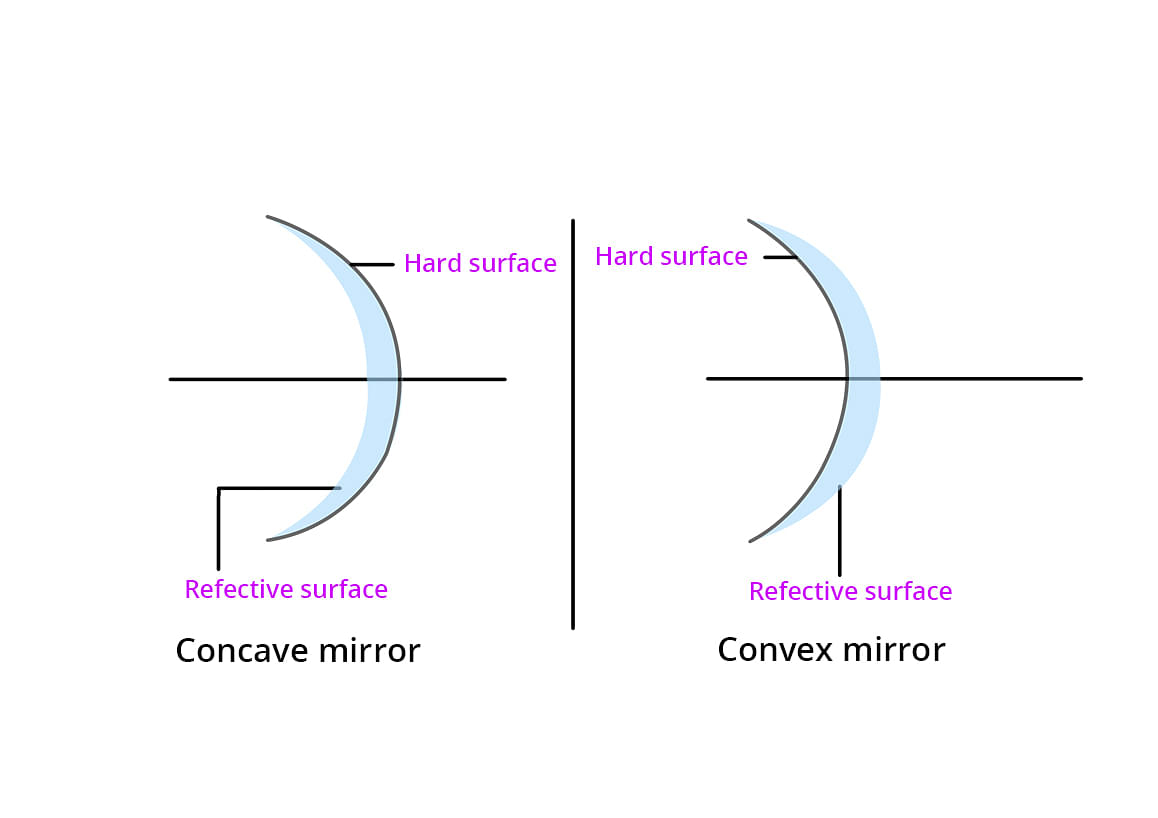
Concave Mirror
Concave mirrors are also called converging mirrors, because in these types of mirrors, light rays converge at a point after impact and reflect back from the reflective surface of the mirror.
Convex Mirror
The convex mirror has a reflective surface that is curved outward. Regardless of the distance between the subject and the mirrors, these mirrors are "always" virtual, upright and reduced.



