A charge q is placed at the center of one of the surface of a cube. The flux linked with the cube is :-
- \( \frac{q}{4\epsilon_0} \)
- \( \frac{q}{2\epsilon_0} \)
- \( \frac{q}{8\epsilon_0} \)
- Zero
The Correct Option is B
Solution and Explanation
1. **Using Gauss’s Law:**
When a charge \( q \) is placed at the center of one face of a cube, it can be visualized that the charge \( q \) contributes equally to two adjacent cubes.
2. **Flux Calculation:**
According to Gauss’s law, the total flux \( \Phi \) due to charge \( q \) in a closed surface is given by:
\[ \Phi_{\text{total}} = \frac{q}{\epsilon_0}. \] Since the charge \( q \) is shared equally between two adjacent cubes, the flux through each cube is:
\[ \Phi = \frac{q}{2\epsilon_0}. \]
Answer: \( \frac{q}{2\epsilon_0} \)
Top Questions on Gauss Law
- An electric field \( \vec{E} = (2x \hat{i}) \, \text{N C}^{-1} \) exists in space. A cube of side \( 2 \, \text{m} \) is placed in the space as per the figure given below. The electric flux through the cube is __________ \( \text{N m}^2/\text{C} \).
- JEE Main - 2024
- Physics
- Gauss Law
- There are two cubical Gaussian surface carrying charges as shown. Find ratio of fluxes through surface \(C_1\) and \(C_2\):

- JEE Main - 2024
- Physics
- Gauss Law
- A cubical Gaussian surface has side of length a = 10 cm. Electric field lines are parallel to x-axis as shown. The magnitudes of electric fields through surfaces ABCD and EFGH are 6kNC-1 and 9kNC-1 respectively. Then the total charge enclosed by the cube is
[Take ε0 = 9 × 10-12 Fm-1]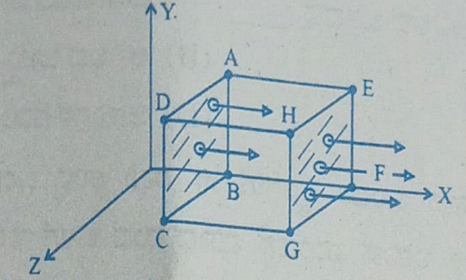
- KCET - 2023
- Physics
- Gauss Law
A cubical volume is bounded by the surfaces $x=0, x= a , y=0, y= a , z=0, z= a$ The electric field in the region is given by $\vec{E}=E_0 x \hat{ t }$ Where $E_0=4 \times 10^4 NC ^{-1} m ^{-1}$ If $a=2 cm$, the charge contained in the cubical volume is $Q \times 10^{-14} C$ The value of $Q$ is ___ Take \(E_{0}=9\times 10^{-2}C^{2}/Nm^{2}\)
- JEE Main - 2023
- Physics
- Gauss Law
- Match List I with List IIChoose the correct answer from the options given below:
LIST I LIST II A Gauss's Law in Electrostatics I \(\oint \vec{E} \cdot d \vec{l}=-\frac{d \phi_B}{d t}\) B Faraday's Law II \(\oint \vec{B} \cdot d \vec{A}=0\) C Gauss's Law in Magnetism III \(\oint \vec{B} \cdot d \vec{l}=\mu_0 i_c+\mu_0 \in_0 \frac{d \phi_E}{d t}\) D Ampere-Maxwell Law IV \(\oint \vec{E} \cdot d \vec{s}=\frac{q}{\epsilon_0}\) - JEE Main - 2023
- Physics
- Gauss Law
Questions Asked in JEE Main exam
- Let \[\vec{a} = \hat{i} + \hat{j} + \hat{k}, \quad \vec{b} = -\hat{i} - 8\hat{j} + 2\hat{k}, \quad \text{and} \quad \vec{c} = 4\hat{i} + c_2\hat{j} + c_3\hat{k} \]be three vectors such that \[\vec{b} \times \vec{a} = \vec{c} \times \vec{a}.\]If the angle between the vector $\vec{c}$ and the vector $3\hat{i} + 4\hat{j} + \hat{k}$ is $\theta$, then the greatest integer less than or equal to $\tan^2 \theta$ is:
- JEE Main - 2024
- Vector Algebra
- 10 mL of gaseous hydrocarbon on combustion gives 40 mL of CO\(_2\)(g) and 50 mL of water vapour. The total number of carbon and hydrogen atoms in the hydrocarbon is ______ .
- JEE Main - 2024
- Hydrocarbons
- If each term of a geometric progression \( a_1, a_2, a_3, \dots \) with \( a_1 = \frac{1}{8} \) and \( a_2 \neq a_1 \), is the arithmetic mean of the next two terms and \( S_n = a_1 + a_2 + \dots + a_n \), then \( S_{20} - S_{18} \) is equal to
- JEE Main - 2024
- Arithmetic Mean
A body of mass 1000 kg is moving horizontally with a velocity of 6 m/s. If 200 kg extra mass is added, the final velocity (in m/s) is:
- JEE Main - 2024
- speed and velocity
- $\textbf{Choose the correct statements about the hydrides of group 15 elements.}$
A. The stability of the hydrides decreases in the order \(\text{NH}_3 > \text{PH}_3 > \text{AsH}_3 > \text{SbH}_3 > \text{BiH}_3\)
B. The reducing ability of the hydrides increases in the order \(\text{NH}_3 < \text{PH}_3 < \text{AsH}_3 < \text{SbH}_3 < \text{BiH}_3\)
C. Among the hydrides, \(\text{NH}_3\) is a strong reducing agent while \(\text{BiH}_3\) is a mild reducing agent.
D. The basicity of the hydrides increases in the order \(\text{NH}_3 < \text{PH}_3 < \text{AsH}_3 < \text{SbH}_3 < \text{BiH}_3\)
Choose the most appropriate from the option given below:- JEE Main - 2024
- p -Block Elements



